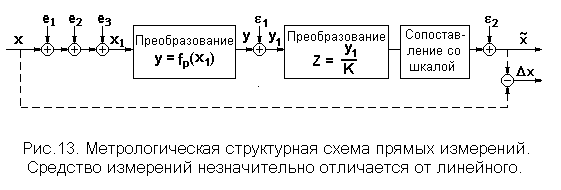
Выше в п. 3.1.3 рассмотрен идеализированный случай линейного средства измерений. Однако в большинстве случаев, несмотря на стремление добиться линейной функции преобразования, все-таки незначительная нелинейность у многих средств измерений остается. Тем не менее, если это целесообразно, подобные средства измерений декларируется в рекламной и сопроводительной документации, как линейные. При этом остаточная нелинейность входит в состав инструментальной погрешности. Рассмотрим эту ситуацию с помощью метрологической структурной схемы, представленной на рис. 13. Эта схема отличается от схемы рис. 10 лишь первой операцией.
|
|
Реальные функции ![]() нелинейного преобразования измеряемой величины, возмущенной погрешностями
нелинейного преобразования измеряемой величины, возмущенной погрешностями ![]() (то есть погрешностями применения) отличаются от линейной функции
(то есть погрешностями применения) отличаются от линейной функции ![]() незначительно, так, что модуль разности между ними при всех значениях измеряемой величины из диапазона измерений не превосходит некоторого значения
незначительно, так, что модуль разности между ними при всех значениях измеряемой величины из диапазона измерений не превосходит некоторого значения ![]() , которое составляет лишь часть общей инструментальной погрешности:
, которое составляет лишь часть общей инструментальной погрешности:
![]() ,
,
где K - номинальный коэффициент преобразования, объявленный в документации.
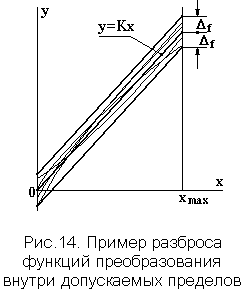
Зона, в которой должны находиться реальные функции преобразования, представлена на рис. 14. Эта зона порождена погрешностями воспроизведения функции преобразования из-за неточности изготовления и старения комплектующих изделий, ее изменением под воздействием внешних влияющих факторов, а также разбросом на множестве экземпляров средств измерений.
Применяя к рассматриваемому случаю обозначения, использованные в (3), получим равенство для абсолютной погрешности измерения:
![]() . (18)
. (18)
По аналогии с неравенством (5) и с теми же обозначениями устанавливаются граничные значения для абсолютной погрешности:
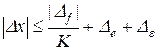 . (19)
. (19)
Как видим, в этом случае, как и в п. 3.1.1, мультипликативная составляющая погрешности не выделяется. В силу непредсказуемого различия реальных функций преобразования у различных экземпляров средств измерений здесь вся погрешность считается аддитивной, и максимально возможное или допустимое значение правой части неравенства (19) принимается в качестве предельного значения погрешности измерений во всем диапазоне измерений.
Простым делением обеих частей неравенства (19) на x мы получаем выражение для пределов допускаемой относительной погрешности:
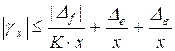 . (20)
. (20)
Для средств измерений с незначительной нелинейностью нормируется приведенная погрешность, то есть абсолютная погрешность, отнесенная к максимальному значению измеряемой величины в диапазоне измерения:
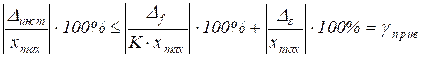
Поможем написать любую работу на аналогичную тему
Реферат
Частная метрологическая структурная схема. Функция преобразования средства измерений незначительно отличается от линейной
От 250 руб
Контрольная работа
Частная метрологическая структурная схема. Функция преобразования средства измерений незначительно отличается от линейной
От 250 руб
Курсовая работа
Частная метрологическая структурная схема. Функция преобразования средства измерений незначительно отличается от линейной
От 700 руб