Метрологическая структурная схема прямых измерений мгновенных значений измеряемой величины с помощью аналоговых средств измерений

Преобразование изменяющихся во времени величин (далее - сигналов), выполняемое физическими устройствами, приводит к искажению формы сигналов вследствие того, что частотная характеристика любого физически реализуемого преобразователя неравномерна, а это означает, что коэффициенты преобразования различных гармонических составляющих входного сигнала различны. С увеличением частоты коэффициент преобразования в конечном итоге уменьшается вплоть до нуля. Во временной области процесс преобразования описывается интегральным оператором типа свертки, который при нулевых начальных условиях имеет вид

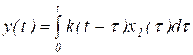                              ,                                    (21)

где k(t-t) называется ядром оператора, а в теории измерений и автоматического управления - импульсной переходной функцией или весовой функцией. Это  преобразование  показано  на  метрологической  структурной  схеме рис. 15, где использованы все обозначения, принятые ранее в п. 3.1.1. Индекс ‘p’ у обозначения импульсной переходной функции означает, что в составе конкретного экземпляра средства измерений используется реальный преобразователь.  Характеристики реальных преобразователей на множестве всех экземпляров имеют разброс, вызванный теми же причинами, которые перечислены выше в п. 3.1.1 в отношении реального коэффициента преобразования.

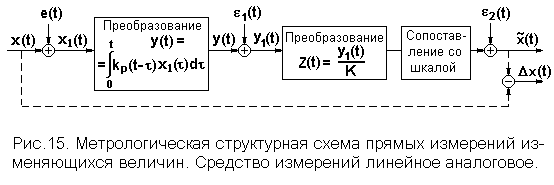
Отличие настоящей схемы от предыдущих состоит лишь в том, что в данной схеме все величины зависят от времени, а погрешности применения, действующие на входе средства измерений, обозначены единым символом e(t).

Сигнал, полученный в итоге первого преобразования, подвергается масштабированию с коэффициентом K, принятым в качестве номинального для данного средства измерений. После этого выполняется сопоставление со шкалой и регистрация значений измеряемой величины на носителе информации (диаграммной ленте, фотопленке, магнитной пленке и т.п.) в единицах ее измерения. В ходе неизбежной расшифровки полученной непрерывной записи результатами измерений оказываются дискретные значения, а в состав погрешности  входит погрешность расшифровки.

В соответствии с приведенной схемой погрешность прямого измерения мгновенных значений изменяющейся измеряемой величины может быть записана в виде равенства

,

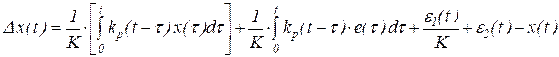откуда

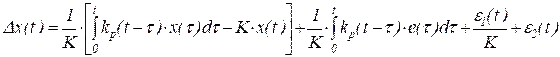. (22)

Применяя к этому равенству преобразование Фурье, получим выражение для комплексного спектра погрешности измерения через спектры сигналов и реальную комплексную частотную характеристику преобразователя :

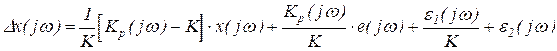, (23)

где частотные характеристики суть преобразования Фурье соответствующих импульсных переходных характеристик:

                    ,      

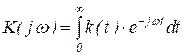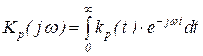
Как видно, структура правой части равенств (22) и (23) аналогична структуре правых частей равенств (3), (4) п. 3.1.1. Мало того, равенство (3) есть частный случай (22) и (23), поскольку при неизменной во времени измеряемой величине  (или  неизменном  сигнале  измерительной  информации), то есть при w = 0

           ,  ,

           ,     .

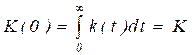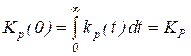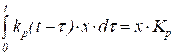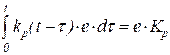Первые слагаемые в правой части каждого из равенств (22) и (23) представляют собой погрешности, вызванные двумя причинами: разбросом импульсных переходных характеристик и комплексных частотных характеристик на множестве экземпляров и их нестабильностью, а также отличием реального преобразования от идеального безинерционного, то есть такого, когда частотная характеристика практически не отличается от единицы, и тогда форма сигнала x(t) не искажается. Эта вторая причина вносит наибольший вклад в погрешность результата измерения мгновенных значений быстропеременных величин, если их спектр выходит за пределы частотной полосы преобразователя.

Вторые слагаемые в формулах (22) и (23) своим происхождением обязаны погрешности применения, которая претерпела то же преобразование, что и измеряемая величина, и если ее спектр выходит за пределы частотной полосы преобразователя, то она частично фильтруется. Получившаяся в результате составляющая погрешности измерения называется наследственной погрешностью.

Последние два слагаемых каждого из равенств (22) и (23) образуют в сумме собственную аддитивную абсолютную погрешность средства измерений.