Характеристики, отражающие влияние прибора на объект.

                   Многим со школьных времён известно положение, которое можно выразить фразой: «Хорош тот вольтметр, у которого сопротивление побольше, а амперметр – у которого поменьше». Теперь поставим вопрос: а собственно говоря, почему это так?

Возьмём вольтметр, измеряющий напряжение постоянного тока.

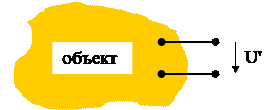Нас интересует напряжение U' между двумя выделенными точками, которое было на объекте до подключения вольтметра.

После того, как вольтметр подключили, напряжение хотя бы совсем немного, но обязательно уменьшится:

	объект

Почему это так?

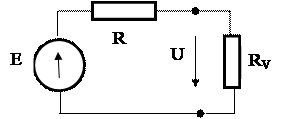
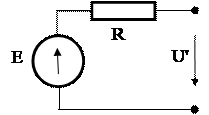
Сколь бы ни была сложна схема объекта, но относительно двух выделенных точек его можно представить в виде активного двухполюсника, содержащего последовательно соединённые э.д.с. Е и сопротивление R. Пока вольтметр ещё не подключён, получаем U' = E, а после подключения

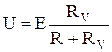,                                                (14)

где RV – сопротивление вольтметра.

         Погрешность от взаимодействия вольтметра с объектом:

            Δвз = U – U' = 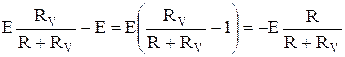.                (15)

Эта формула неудобна тем, что э.д.с. Е нам не известна, мы знаем U, а не Е. Но из формулы (15) можно выразить Е:

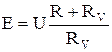      .                                                       (16)

Подставив (16) в (15), получим:

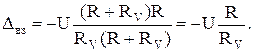                                                                        (17)

При RV → ∞ погрешность взаимодействия Δвз → 0. Вот почему хорош тот вольтметр, у которого побольше RV: у него поменьше Δвз.

Заметим, что Δвз → 0 также и при RV → 0 (измерение э.д.с.).

Выразим относительную погрешность взаимодействия:

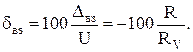                                                                                   (18)

         Аналогичным путём можно найти погрешность взаимодействия амперметра с объектом. При этом должен получиться такой результат: погрешность взаимодействия Δвз → 0 при сопротивлении амперметра RА → 0. Полезно проделать этот анализ самостоятельно. В данном случае удобнее представить эквивалентную схему объекта не в виде последовательного соединения э.д.с. и сопротивления, а в виде параллельного соединения источника тока и сопротивления.

         Таким образом, RV и RA влияют на точность: от них зависит Δвз. Но она зависит не только от них, а ещё и от сопротивления объекта R. Поэтому Δвз или δвз нельзя указать заранее для данного вольтметра или амперметра. Характеристикой прибора, отражающей его влияние на объект, является RV или RA.

         Если измеряется синусоидальное напряжение, то на высоких частотах надо учитывать не только сопротивление RV, но и ёмкость СV. Они включены параллельно. Будем считать, что объект характеризуется чисто активным сопротивлением R.

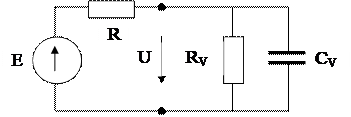
Введём комплексное напряжение  и комплексную э.д.с. :

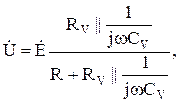
где

.

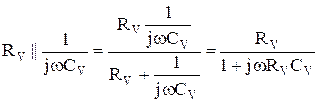 Тогда

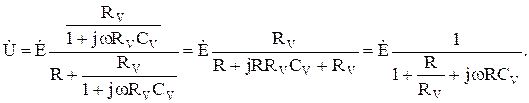
Теперь перейдём к модулям U и Е:

.

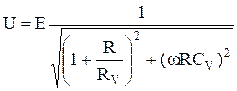Погрешность взаимодействия вольтметра с объектом:

Δвз = U – E = E,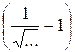

где

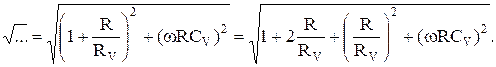
Поскольку R << RV,

.

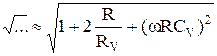Как и раньше, выразим Е через U:

Е = U

и подставим в формулу для Δвз:

Δвз = U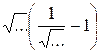 = U(1 .

Поскольку Δвз << U (иначе измерение бессмысленно),  << 1, т.е

 где ε << 1, значит,  пользуясь свойством малых величин, можно написать . Следовательно,

       Δвз = U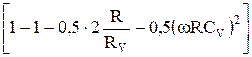 = 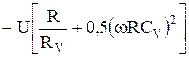.       (19)

При ω = 0 получаем формулу (17). При увеличении ω второе слагаемое быстро растёт !

Мы закончили рассматривать характеристики измерительных приборов. Теперь вкратце о других средствах измерений: мерах и измерительных преобразователях.

Меры.

Первая характеристика меры – её номинальное значение Yном, для многозначной меры – множество номинальных значений.

Абсолютная погрешность меры: Δ = Yном – Yист ≈ Yном – Yд, где Yист и Yд - истинное и действительное значения меры.

Для однозначных мер относительная погрешность δ и приведённая погрешность γ – одно и то же, для многозначных соотношение между ними такое же, как у измерительных приборов.

Для тех и других сохраняются понятия систематической Δс и  случайной  составляющих.

Измерительные преобразователи.

         Главная характеристика измерительного преобразователя – номинальная функция преобразования :

                       Y = fном (Х).

Она может быть в виде формулы или таблицы или графика. Частный случай – линейная функция, проходящая через начало координат. Здесь достаточен номинальный коэффициент преобразования:

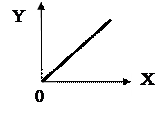                            Sном = .

Для измерительных преобразователей остаются в силе понятия о трёх формах выражения погрешности – абсолютная Δ, относительная δ и приведённая γ; понятия об основной погрешности Δо и о дополнительных погрешностях Δд; понятия о систематической Δс и случайной  составляющих. Но, кроме того, здесь действуют ещё два, которых нет у измерительных приборов и у мер: погрешность на входе Δвх и погрешность на выходе Δвых.

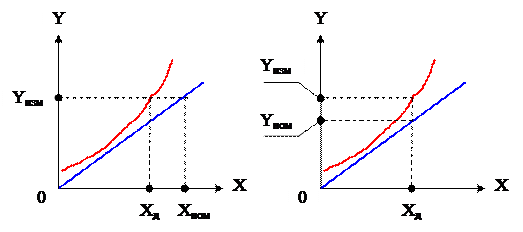
Синяя линия – номинальная функция преобразования, которой мы располагаем, а красная – реальная, которая, вообще говоря, нам не известна. Сначала обратимся к левому рисунку. Если на выходе преобразователя мы получили, например, измерили некоторое значение выходного сигнала Yизм, то, пользуясь номинальной функцией, мы «думаем», что на входе действует сигнал со значением Хном. На самом же деле его действительное значение Хд. Абсолютная погрешность на входе («измеренное – в данном случае номинальное – минус действительное»):

Δвх = Хном – Хд.

Теперь посмотрим на правый рисунок. Пусть входной сигнал имеет некоторое действительное значение Хд. На выходе ему соответствует сигнал со значением Yизм, которое можно измерить. Значение же выходного сигнала Yном можно ещё назвать идеальным: оно было бы на выходе, если бы преобразователь был без погрешностей. В некотором смысле оно аналогично действительному, а точнее говоря, истинному значению в случае измерительного прибора: прибор показал бы это значение, если бы он был без погрешностей. Абсолютная погрешность на выходе («измеренное минус действительное – в данном случае номинальное»):

Δвых = Yизм – Yном.