Виды и методы измерений

Виды измерений:

• Прямые
• Косвенные
• Совокупные
• Совместные

Прямые – искомое значение физической величины  получают непосредственно из опыта.

Примеры: измерение длины линейкой; измерение тока амперметром и т.п., т.е. все обычные измерения.

Косвенные – искомое значение физической величины вычисляют на основании известной зависимости этой величины от нескольких других, значения которых получены прямыми измерениями.

Пример: вычисление сопротивления R по измеренным значениям напряжения U и тока I.

Замечание: измерение сопротивления омметром – это прямое измерение.

Совокупные и совместные – одновременное измерение нескольких величин и нахождение искомых значений путём решения системы уравнений.

При совокупных измеряемые величины одноимённые, при совместных – не одноимённые.

Пример совокупных измерений:

                                                       Треугольник разрывать нельзя.

                                                       Измеряют сопротивления RAB ; RBC; RAC

                                                       между точками А, В, С, составляют систему               

                                                       трёх уравнений с тремя неизвестными

                                                       и находят R1; R2;  R3.

Пример совместных измерений:

R = R0(1 + αθ),

где R – сопротивление при температуре θ; R0 – значение R при θ = 0; α – температурный коэффициент.

Искомыми являются R0 и α. Измеряют два значения R:

R = R1 при θ = θ1 и R = R2 при θ = θ2. Решение системы двух уравнений

R1 = R0(1 + αθ1)

R2 = R0(1 + αθ2)

даёт искомые значения R0 и α.

Если

R = R0(1 + αθ + βθ2),

то для нахождения R0; α и β нужны три уравнения.

Замечание. Иногда совокупные и совместные измерения считают частными случаями косвенных.

Методы  измерений:

• Метод непосредственной оценки (мера в явном виде не присутствует, она отражена в шкале). Примеры: пружинные весы, амперметр со стрелкой и шкалой и т.п.
• Методы сравнения с мерой (она присутствует в явном виде):

– нулевой метод;

         – дифференциальный метод;

         – метод замещения;

         – метод совпадений.

Методы сравнения с мерой более точные, но и более медленные.

Нулевой метод. Разность между измеряемой величиной и величиной, воспроизводимой мерой, доводится до нуля.

Примеры: рычажные весы с гирями; равновесный мост; компенсатор.

Равновесный мост постоянного тока:

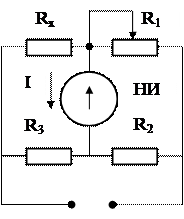Изменением R1 уравновешивают мост, т.е. добиваются отсутствия тока в нуль-индикаторе НИ. Легко показать, что при этом Rx R2 = R1 R3.

Отсюда измеряемое сопротивление Rx = .

Обратите внимание, что при изображении НИ на схемах стрелку внутри окружности рисуют вертикально.

Дифференциальный метод. Разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряется прибором непосредственной оценки.

Примеры: пружинные весы с маленькой платформой, на которую ставят гирю, когда масса на большой платформе превышает диапазон измерения по шкале; неравновесный мост.

Неравновесный мост постоянного тока:

при ΔR = 0 изменением R1 мост уравновешен    при R0R2 = R1R3; далее при ΔR ≠ 0 значение ΔR преобразуется в ток I.

Неравновесные мосты широко применяются при измерении не электрических величин. Измеряемая величина преобразуется в ΔR измерительным преобразователем. Например, температура преобразуется в изменение сопротивления терморезистора.

Метод замещения. Измеряемую величину замещают известной, и измеряют поочерёдно.

Пример: Rx – искомое сопротивление; R0 – известное. Поочерёдно измеряют напряжения Ux и U0.

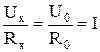     ; Rx = R0.     

      Ток I не нужно точно устанавливать, не нужно знать его значение.

Метод совпадений. Разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадение отметок шкал или периодических сигналов.

Примеры: штангенциркуль с нониусом; стробоскоп – метка на вращающемся теле освещается вспышками лампы и кажется неподвижной, когда частота вспышек равна (или кратна) частоте вращения.