Точность

Количественная характеристика точности – погрешность. Чем меньше погрешность, тем выше точность.

Прежде всего, существуют два понятия:

• погрешность измерения;
• погрешность измерительного прибора.

Это не одно и то же. Можно взять дорогой, очень точный прибор, но получить при неграмотном использовании очень плохой результат. Попробуйте сами привести пример такой ситуации.

Существует три формы выражения погрешностей:

• абсолютная Δ;
• относительная δ:
• приведённая γ.

Погрешность измерения может быть выражена в форме Δ или δ, а погрешность измерительного прибора – в любой из трёх форм.

         Абсолютная погрешность измерительного прибора:

      Δ = Х – Хист ≈ Х – Хд,                                         (6)

где Х – показание прибора; Хист – истинное значение измеряемой величины;

Хд – её действительное значение.

         Относительная погрешность измерительного прибора:

δ = 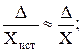 δ (%) = 100                                    (7)

Приведённая погрешность измерительного прибора:

γ =  γ (%) = 100·                                  (8)

где Хн – нормирующее значение измеряемой величины.

Что значит «нормирующее значение? Покажу на примерах:

1) У вольтметра с диапазоном измерения от 0 до 15 В нормирующее значение

Хн = Uн = 15 В.

2) У миллиамперметра с двусторонней шкалой – 5 мА ÷ 0 ÷ 5 мА нормирующее значение

Хн = Iн = 5 мА (или 10 мА).

3) Частотомер с узким диапазоном измерения 49 Гц ÷ 50 Гц ÷ 51 Гц  нормирующее значение

Хн = fн = 50 Гц.

         Связь относительной погрешности с приведённой:

δ = γ· δ = γ при Х = Хн ; δ > γ при Х < Хн !

         Основная погрешность и дополнительные погрешности.

         Погрешность Δ зависит от влияющих величин ξ:

Δ = f(ξ1; ξ2;… ξn).

Влияющие величины – это:

а) внешние факторы – температура, напряжение питания (если оно есть у прибора) и др.;

б) неинформативные параметры входного сигнала.

Пример: u(t) = Umsinωt = Usin2πft

– вольтметром измеряют среднее квадратическое значение U синусоидального напряжения u(t); в этом случае частота f этого напряжения – неинформативный параметр входного сигнала, т.е. такой параметр, который не несёт полезной информации о значении U, но влияет на результат измерения U;

– частотомером измеряют частоту f синусоидального напряжения u(t); в этом случае U – неинформативный параметр входного сигнала.

         Нормальные условия применения прибора – это такие условия, когда все влияющие величины ξi либо имеют нормальные значения

ξi = ξi,норм,

либо находятся в пределах нормальных областей значений

ξi,норм,min ≤ ξi ≤ ξi,норм,max.

Примеры:

а) θ = 20 0С – нормальное значение температуры, принятое в нашей стране;

б) относительная влажность воздуха от 30 до 80 % – нормальная область значений.

Примечание. Обеспечить при испытаниях точно 20 0С невозможно, поэтому допускаются отклонения, например, в пределах (20 ± 2) 0С. Этот допуск зависит от точности испытуемого прибора; для самых точных он составляет ± 0,5 0С.

ОСНОВНАЯ погрешность Δо – это погрешность в нормальных условиях.

         Рабочие условия применения прибора – это такие условия, когда влияющие величины ξi находятся в пределах рабочих областей значений

ξi,раб,min ≤ ξi ≤ ξi,раб,max.

Пример:

температура в пределах 10 0С ≤ θ ≤ 35 0С (2я группа средств измерений)

                                            ·

                                            ·

                                            ·

                                       – 50 0С ≤ θ ≤ 60 0С (6я группа).

ДОПОЛНИТЕЛЬНАЯ погрешность Δд – это изменение погрешности, вызванное отклонением одной из влияющих величин ξi от её нормального значения ξi,норм или выходом за пределы нормальной области значений ξi,норм,min ÷ ξi,норм,max.

 Систематическая и случайная погрешности.

Систематическая погрешность Δс остаётся постоянной или закономерно изменяется  в зависимости от времени (или другого аргумента).

Случайная погрешность  изменяется случайным образом.

Пусть Х = const. Производятся повторные измерения Х. Если              Х1; Х2;…Хn отличаются друг от друга – значит, проявляет себя случайная погрешность. Что при этом принять за результат измерения? Ответ известен: среднее значение:

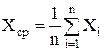.                                                (9)

          В вероятностном смысле Хср ближе к истинному значению Хист, чем любое Хi. Это объясняется тем, что одни Хi отличаются от Хср в одну сторону, другие – в другую. Чем больше n, тем меньше влияние случайной погрешности, но тем дольше процесс измерения.

          Такое измерение с повторами и усреднением называют измерением с многократными наблюдениями: Хi – это наблюдения, а Хср – результат измерения.

          Таким образом, простой приём – многократные наблюдения – позволяет обнаружить присутствие случайной погрешности, а их усреднение – снизить её влияние.

          Заметим, что этот приём не обнаруживает систематическую погрешность и не снижает её.

          Для нахождения Δс нужен более точный прибор, показание которого можно считать действительным значением Хд, и тогда              

                Δс = Х – Хд                                                 (10)

или

      Δс = Хср – Хд,                                             (11)

если выявлено присутствие случайной погрешности и произведены многократные наблюдения.

Если Δс найдена, её можно исключить, введя поправку:

η = – Δс.                                                 (12)

Тогда Х + η – это будет исправленный результат измерения.

Получается, что если погрешность найдена – это уже не погрешность. Погрешность остаётся погрешностью лишь до тех пор, пока в ней есть неопределённость, случайность. После внесения поправки остаются не исключённые остатки Δс, но они уже случайны.

Итак, погрешность – в принципе случайная величина.

Случайные величины можно изучать, у них есть определённые законы. Этим занимается одна из отраслей математики – теория вероятностей. Мы будем её использовать.

Мы рассмотрели случай, когда с помощью более точного прибора находят Δс и вводят поправку η. Может возникнуть вопрос: если у нас есть этот более точный прибор, почему бы им и не измерять? Дело в том, что поправка вносится в результаты многих измерений, а определяется редко. Для её нахождения используются эталонные средства измерения. Они служат не для измерений, а для поверки и аттестации рабочих средств измерения. Если бы эталонные средства использовались для измерений, они быстро бы перестали быть эталонными.

Но вообще внесение поправки – довольно редкий случай в практике измерений: это точные лабораторные измерения, научные исследования. Большей частью Δс есть, но её не выявляют для каждого данного экземпляра средств измерений. На множестве экземпляров данного типа средств измерений она проявляет себя, как случайная величина.

Таким образом, проявляет себя, как случайная величина на множестве многократных наблюдений, если таковые производятся, а Δс проявляет себя, как случайная величина даже при одном измерении – на множестве экземпляров приборов данного типа.

Нормирование погрешностей

          Нормируют предельно допускаемые значения погрешностей средств измерений, в первую очередь для основной погрешности. Существуют разные формы нормирования:

1) Нормируют предельно допускаемые значения основной приведённой погрешности, например, γо,п = ± 0,5 %. Так нормируют погрешности аналоговых вольтметров, амперметров и т.п. Это означает, что – 0,5 % ≤ γо ≤ 0,5 %.

Возможно, нам попался экземпляр прибора, у которого γо = 0, но мы этого не знаем. Мы знаем, что гарантируется – 0,5 % ≤ γо ≤ 0,5 %.

2) Гораздо реже гарантируется предельно допускаемые значения основной относительной погрешности, например, δо,п = ± 0,02 %. Так, например, нормируют погрешность измерительных мостов.

3) Нормируют предельно допускаемые значения основной относительной погрешности, но не в виде числа со знаками ±, а в виде формулы:

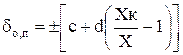     .                                        (13)

Так нормируют погрешность для цифровых измерительных приборов, например:

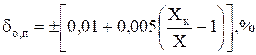
Дополнительные погрешности.

Рассмотрим на примерах.

Пример 1.

В документации читаем: «Дополнительная температурная погрешность не более половины основной на каждые 10 0С в рабочем диапазоне». Расшифруем эту фразу. Пусть известно, что для данного прибора:

– рабочий диапазон температур 5 0С ≤ θ ≤ 40 0С;

– предельные значения основной приведённой погрешности γо,п = ± 0,5 %.

Это значит, что при 10 и при 30 0С к γо добавляется ещё ± 0,25 %. Есть основания считать, что зависимость дополнительной температурной погрешности от температуры близка к линейной. Поэтому, если, например, θ = 35 0С, то предельные значения дополнительной температурной приведённой погрешности будут

.

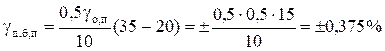Здесь  – температурный коэффициент дополнительной температурной погрешности.

Если бы вместо «…не более половины основной…» было «…не более основной…», то температурный коэффициент был бы 0,1γо,п.

Пример 2.

          В документации читаем: «Дополнительная частотная погрешность не более основной». Пусть это относится к аналоговому вольтметру переменного напряжения, у которого нормальная область значений частоты                  45 Гц ≤ fнорм ≤ 1 МГц, а рабочая область 20 Гц ≤ fраб ≤ 5 МГц. На циферблате прибора это обозначается так:

20 Гц…45 Гц…1 МГц…5 МГц

Пусть для этого вольтметра γо,п = ± 4 %. Это значит, что в диапазонах от        20 Гц до 45 Гц и от 1МГц до 5 МГц к γо добавляется дополнительная частотная погрешность с предельными значениями γд,f,п = ± 4 %. В случае частотной погрешности нет оснований считать, что она линейно зависит от частоты. Поэтому, если, например, f = 2 МГц всё равно приходится считать, что при этом γд,f,п = ± 4 %.

Это, конечно, плохо, поэтому стандарт предлагает нормировать не дополнительные погрешности, а функции влияния (для линейных функций – коэффициенты влияния).

Классы точности

                   Класс точности – комплексная характеристика, которая говорит нам и об основной и о дополнительных погрешностях .

Обозначение классов точности:

• На циферблате аналогового прибора проставлено число, например, 0,5. Что оно означает? В первую очередь, что γо,п = ± 0,5 %.
• На лицевой панели прибора проставлено число внутри окружности, например,

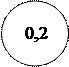
     Это значит, что δо,п = ± 0,2 %.

• В документации цифрового измерительного прибора его класс точности обозначен 0,01/0,005. Это значит, что

.

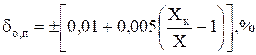Все числа, фигурирующие в обозначениях классов, выбираются из ряда

(1; 1,5; 2; 2,5; 4; 5; 6)·10а,

где а = 1; 0; – 1; – 2; …

                   Кроме основной погрешности класс точности даёт информацию о дополнительных погрешностях, например, так, как это было показано в приведённых выше примерах, но как именно, в частности, «…не более половины основной…» или «…не более основной…» – это надо уточнять по документации на прибор.