Часто при измерениях заранее известно, что возможные значения случайных погрешностей средства измерения равновероятны и лежат в пределах некоторого определенного интервала. Такое распределение называется равномерным. Значения дифференциальной функции такого распределения в определенном интервале {-α; +α] постоянны, а вне этого интервала равны нулю. Дифференциальная функция распределения случайной погрешности в этом случае имеет вид:
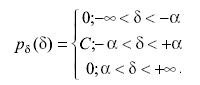(3.35)
Такая ситуация встречается каждый раз, когда речь идет об измерениях величины, изменяющейся порциями, квантами. В оптике это изменения энергии в пределах энергии кванта ΔЕ = hν. В электричестве это, например, изменения заряда в пределах заряда электрона е. В механике дискретность массы определяется массой одной частицы. Та же самая ситуация имеет место при измерениях прибором, разрешающая способность которого хуже, чем статистический разброс случайных значений величины. В этом случае всегда при изменениях величины меньшем, чем разрешающая способность прибора, мы получим одно и то же значение, а вероятность отклонения величины в этих пределах измерить будет невозможно.
То же самое имеет место при измерениях размеров калибрами, т. е. концевыми мерами или скобами сфиксированными параметрами. Например, имея концевую меру в виде щупа или плитки Иогансона, мы можем рассортировать предметы только по признаку больше они по размеру номинала щупа или плитки или меньше. Поскольку калибры, щупы и плитки Иогансона являются такими же средствами измерения, как показывающие или регистрирующие приборы, в измерительной практике нужно уметь оценивать погрешности и при их использовании.
Постоянную величину С в равномерном распределении находят из условия, что площадь между кривой распределения и осью абсцисс должна равняться единице, т. е.:
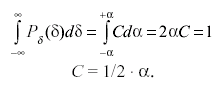(3.36)
Уравнение для интегральной функции равномерного распределения находится из условия, что Fδ(δ) = 0 до тех пор, пока δ< -α. В пределах интервала :
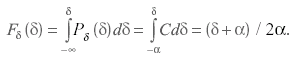(3.37)
Это означает, что интегральная функция равномерного распределения растет от значения Fδ(δ)=0 при δ= -α до Fδ(δ)=1 при δ=+α. При прохождении абсциссы через нуль интегральная функция равна 0,5. Окончательное выражение для интегральной функции распределения имеет вид:
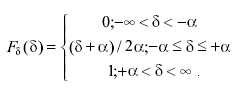(3.38)
Математическое ожидание случайной погрешности при равномерном распределении легко найти из его определения:
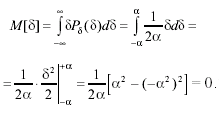(3.39)
Дисперсию случайной равномерно распределенной погрешности можно найти по формуле:
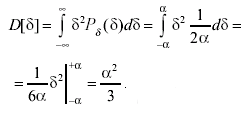(3.40)
Вероятность попадания случайной погрешности в заданный интервал (δ1; δ2] при равномерном распределении равна
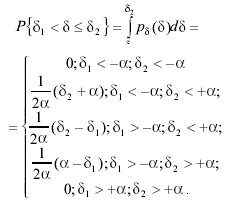(3.41)
На графике функции распределения эта вероятность равна заштрихованной на рис. 3.5 площади.
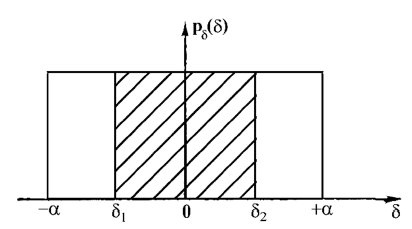
Если интервал изменения δ полностью укладывается внутри интервала изменения а, то искомая вероятность просто равна отношению длин этих интервалов. Если интервал изменения δ находится полностью за пределами интервала изменения α, то вероятность попадания случайной погрешности в интервал (δ1; δ2] равна нулю.
Поможем написать любую работу на аналогичную тему