Нормальное распределение Гаусса

В большинстве практических случаев при чисто случайных разбросах результатов отдельных измерений относительно истинного значения измеряемой величины функция распределения имеет вид, получивший название нормального распределения Гаусса.

Если причины, вызывающие отклонения результатов измерения от истинного значения, настолько разнообразны и многоплановы, что невозможно выделить какую-либо доминанту, функция распределения всегда имеет вид экспоненты с определенными параметрами. К этому утверждению следует относиться как к аксиоме физики, т. е. мир устроен так, что при случайном выпадении многократных результатов повторяющихся событий функция распределения будет иметь вид экспоненты. В метрологии, как и в физике вообще, встречается достаточно много аксиом, например постоянство скорости света, корпускулярно-волновой дуализм, токи смещения в уравнениях Максвелла, принцип относительности и т. д. Аналитическую зависимость функции нормального распределения можно отнести к категории таких принципов или аксиом. В метрологии и в технике измерений получение такой зависимости неоценимо в определении достоверности, правильности и точности измерений. Предложенная Гауссом зависимость дифференциальной функции распределения результатов повторяющихся случайных событий оказалась настолько ценной, что в Германии, например, формула нормального распределения считается одним из самых крупных достижений науки.

Нормальное распределение выпадения определенного результата в повторяющихся случайных событиях это такое распределение, дифференциальная функция распределения которого имеет вид:

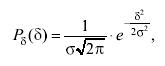(3.42)

где δ = х - mF; здесь: х - результат однократного измерения; mF - математическое ожидание результата измерения так, что

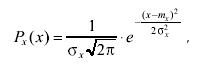(3.43)

где σx - среднее квадратическое отклонение результатов измерения.

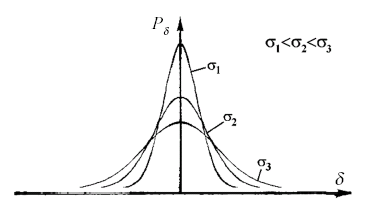
При записи в таком виде кривые нормального распределения зависят от среднего квадратического отклонения. При увеличении σ распределение все более расплывается, т. е. вероятность появления больших отклонений от математического ожидания увеличивается, а вероятность меньших погрешностей сокращается (рис.).

Для того чтобы сделать аналитическую зависимость нормального дифференциального распределения более универсальной, делают замену переменных, выражая отклонения величины х от математического ожидания mF в единицах среднего квадратического отклонения:

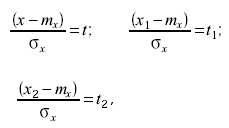(3.44)

где х - результат отдельного измерения; x1 - минимальное возможное значение измерения; x2 - максимальное возможное значение измерения. После такой замены переменных вероятность попадания результата измерения в некоторый заданный интервал (x1 ; x2 ] выражается как:

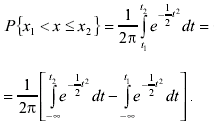(3.45)

Интегралы в скобках не выражаются в элементарных функциях. Их вычисляют с помощью так называемого нормированного нормального распределения с дифференциальной функцией

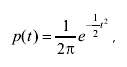(3.46)

график которой изображен на рис.

.

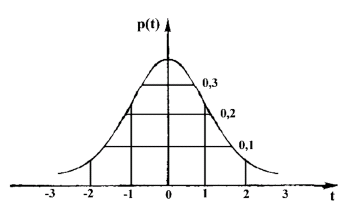
Функция p(t) не зависит от параметров распределения, в силу чего может быть затабулирована. Интегральная функция нормального распределения имеет вид:

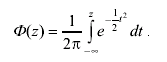(3.47)

По физическому смыслу это есть вероятность того, что погрешность измерения будет меньше или равна величине z, т. е.

(3.48)

Интегральная функция нормального распределения также затабулирована. Используя интегральную функцию нормального распределения, можно определить вероятность попадания результата измерения в интервал (x1 , x2 ] как

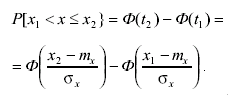(3.49)

При этом справедливо тождество:

(3.50)

Подчеркнем, что все сказанное справедливо, если погрешности случайные, распределение можно считать нормальным с известной дисперсией σx2 . Тогда на основании формулы (3.44) имеем:

(*)

Обычно значения t1 и t2, выбирают симметрично по обе стороны от максимума распределения так, что t1 = t2 = tp. Формула для вероятности попадания результата в заданный интервал приобретает вид:

(3.52)

Меняя х и mF местами в этом неравенстве, получим:

(3.53)

Если систематические погрешности исключены и mF = Q, то

(3.54)

Это означает, что истинное значение измеряемой величины с доверительной вероятностью Р = 2Ф(tp) -1 находится между границами интервала . Интервал от -tpσx до +tpσx называется доверительным интервалом погрешности измерения, а половина интервала tpσx называется доверительной границей случайного отклонения результатов наблюдения, соответствующей доверительной вероятности Р.

Для определения доверительной границы задаются доверительной вероятностью Р и по (*) находят из таблиц параметр tp. После этого вычисляют доверительное отклонение tpσx . Если известно среднее квадратическое отклонение результатов измерения, то легко определить погрешность измерения при заданной доверительной вероятности.

Задача может быть поставлена иначе, а именно: какова доверительная вероятность попадания результата измерения в заданный доверительный интервал, если известно среднее квадратическое отклонение серии измерений? В этом случае определяют параметр tp делением доверительного интервала на среднеквадратическое отклонение tp= (tpσx ) /σx . Затем из таблиц значений интегральной функции нормального распределения находят величину Ф(tp), после чего вычисляют доверительную вероятность как 2Ф(tp) -1.

Из приведенных определений понятий, определяющих нормальное распределение вероятности получения определенных результатов измерения можно кратко сформулировать следующие выводы:

1. Погрешности измерения (интервалы допустимой погрешности) зависят от того, с какой вероятностью мы хотим получить достоверный результат.

2.      Для определения погрешности при заданном доверительном интервале и для определения этого интервала при заданной доверительной вероятности необходимо знать среднее квадратическое отклонение результатов измерения.

3.      Функции нормального распределения дают связь между вероятностью попадания результатов измерения (доверительной вероятностью) в заданный интервал и величиной самого интервала, называемого доверительной границей случайного отклонения.