Нормальное распределение

Плотность распределения:                                                     (45.4).

Точки перегиба кривой плотности распределения:  и .

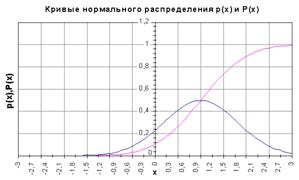Функция распределения:

              (46.4),

где  - м.о., s(х) – стандарт.

Чем больше s(х), тем ниже и шире кривая плотности распределения.

Плотность n-мерного нормального распределения: , где D - определитель корреляционной матрицы , а Ajl – алгебраическое дополнение элемента kjl-того определителя.

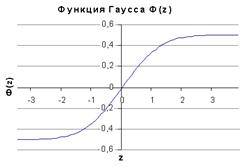
Р(х) можно выразить через интеграл вероятности Гаусса

,                                                (47.4)

                                                             (48.4).

Функция (47) – нечетная (Ф(-z) = - Ф(z)),  имеются таблицы ее значений.

Вероятность попадания с.в. Х в интервал (a,b) –

                                                      (49.4).

Если b-a =6 s(X), то вероятность того, что с.в. Х окажется в интервале  равна 0.9973. Линейные функции с.в., подчиняющиеся нормальным законам распределения, имеют также нормальный закон распределения.

Как показал Ляпунов в случае, если число n безгранично увеличивается, кривая плотностей вероятностей суммы не зависит от кривых плотностей вероятностей, слагаемых при некоторых предположениях, и представляет собой нормальную кривую (45.4).

Условия: слагаемые величины х=х1+х2+...+хn (xi, i=1, 2...n) в среднем одного порядка и одного порядка некоторые характеристики слагаемых - вторые и третьи моменты. Т.о. если с.в. образуется из суммы большого числа независимых, неограниченных случайных переменных факторов, то ее закон - близок к нормальному, т.е. в действительности многие переменные представляют собой результат простого суммирования многих независимых факторов.

.