Методы измерений - Дисциплина метрология – шпаргалки к экзамену.

Чтобы выполнить измерение в соответствии с решаемой задачей, применяют различные методы измерений.

Метод измерения - путь, способ экспериментального нахождения значения физической величины, т.е. совокупность приемов использования физических явлений, на которых основаны измерения. Различают два основных метода измерения.

Метод непосредственной оценки - метод измерений, при котором значение величины определяют непосредственно по отсчетному устройству средства измерений. Иногда метод непосредственной оценки еще называют методом прямого преобразования, так как он основан на известной функциональной зависимости между показанием средства измерений и входным сигналом.

Наиболее многочисленными средствами измерений, служащими для измерения методом непосредственной оценки, являются аналоговые измерительные приборы, в частности стрелочные показывающие приборы. К стрелочным показывающим приборам можно отнести манометры, динамометры, барометры, амперметры, вольтметры, фазометры, ваттметры и многие другие. Следует отметить, что хотя удельный вес цифровых показывающих приборов в общей совокупности выпускаемых средств измерений непрерывно растет, применение стрелочных показывающих приборов вовсе не стремится к нулю. Это объясняется тем, что данные приборы проще по конструкции, дешевле, да пока и надежнее, чем цифровые, но не только этим. Одна из причин принципиального характера кроется в том, что на практике не так уж редки ситуации, когда стрелочная форма индикации предпочтительнее цифровой. Сюда можно отнести режимы слежения за поведением измеряемой величины, например, контроль постоянства уровня величины.

Метод сравнения - метод, при котором измеряемую величину сравнивают с известной величиной, воспроизводимой мерой.

Метод сравнения реализуется в измерительной практике в виде следующих основных модификаций:

нулевой метод, при котором результирующий эффект воздействия обеих величин на измерительный прибор доводится до нуля (этот метод часто также

называют компенсационным);

дифференциальный метод, при котором образуют и измеряют разность измеряемой и известной величин;

метод замещения, при котором измеряемую величину замещают в процессе измерений известной величиной;

метод совпадений, при котором образуют разность измеряемой и известной величин и оценивают ее по совпадениям или биениям.

Примером средств измерений, в которых используется нулевой метод, являются мосты для измерения сопротивления, емкости и индуктивности. На рисунке 3.1 показана схема моста для измерения сопротивления Rx. Схема состоит из трех сопротивлений с известными значениями (R2 , R3 и R4), измеряемого сопротивления Rx, нуль–индикатора НИ и источника постоянного тока ИПТ. Изменяя одно из известных сопротивлений, например R4, добиваются нулевого показания НИ. Это может быть только тогда, когда между точками 2-4 нет разности потенциалов, или, другими словами, падение напряжения между точками 1-2 равно падению напряжения между точками 1-4. Как следствие падения напряжения между точками 2-3 и 3-4 также равны между собой. На основании этих равенств можно определить измеряемое сопротивление Rx, зная известные сопротивления R2, R3 и R4,

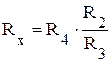.                                                   (3.4)

Дифференциальный метод, например, используется при поверке измерительных трансформаторов тока. Принципиальная электрическая схема поверки показана на рисунке 3.2.

Для определения погрешности коэффициентов трансформации поверяемый трансформатор тока Тх сравнивают с образцовым T0. Первичные обмотки обоих трансформаторов включены в цепь одного и того же тока I1. Вторичные обмотки включены таким образом, что их токи Ix и I0 направлены навстречу друг другу. Разность между этими токами, измеряемая при помощи измерительного прибора ИП, пропорциональна разности коэффициентов трансформации, т.е. погрешности коэффициента трансформации поверяемого трансформатора Тх.

Приведенная на рисунке 3.2 схема является упрощенной. В конструкцию установок для поверки измерительных трансформаторов дифференциальным методом введен ряд дополнений, которые позволяют определять не только погрешность коэффициента трансформации, но и погрешности угла сдвига фаз между токами в первичной и вторичной цепях. Аналогичная схема применяется и для поверки измерительных трансформаторов напряжения.

Применение метода замещения позволяет исключить ряд систематических погрешностей, возникающих в процессе измерения в некоторых средствах измерений. Например, для измерения емкости Сх на высоких частотах используется резонансный измеритель контурного типа.

Упрощенная структурная схема такого измерителя в режиме измерения Сх приведена на рисунке 3.3. В простейшем случае достаточно образовать колебательный контур из Сх и образцовой катушки индуктивности L0 (Сx подключается к зажимам 4-5, емкость регулируемого образцового конденсатора С0 устанавливается на минимальное значение), настроить контур в резонанс по показанию индикатора резонанса ИР изменением частоты измерительного генератора ИГ и, отсчитав значение резонансной частоты (fр) по шкале ИГ, определить Сx по общеизвестной формуле

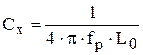.                                              (3.5)

Однако при таком способе измерения существенное влияние на точность измерения оказывают паразитные параметры контура (особенно паразитные емкости) и мы фактически измеряем не Сх, а емкость контура. Поэтому при измерении резонансный метод сочетают с методом замещения.

При использовании этого сочетания после установки требуемой частоты ИГ настраивают в резонанс контур, образованный С0 и L0, изменяя С0 до значения С01. Затем к зажимам 4-5 подключают Сх и вновь настраивают контур в резонанс на той же частоте, уменьшая С0 от значения C01 до значения С02. Очевидно, в этом случае

Cx=C01-C02,                                                  (3.6)

систематические погрешности, обусловленные паразитными емкостями контура, исключаются из результата измерения Сх, так как они входят с одинаковыми значениями и знаками в С01 и С02.

Метод совпадений характеризуется использованием совпадения отметок шкал и периодических сигналов. Например, по принципу метода совпадения построен нониус штангенциркуля и ряда других приборов. Шкала нониуса штангенциркуля имеет десять делений по 0,9 мм. Когда нулевая отметка шкалы нониуса окажется между отметками основной шкалы штангенциркуля, это будет означать, что к целому числу миллиметров следует прибавить некоторое число х десятых долей миллиметра (рис. 3.4). Так как измеряемая дробная часть миллиметра 0,1·х равна разности между целым числом миллиметров по основной шкале штангенциркуля (п мм) и расстоянием по шкале нониуса от нулевой до совпадающей отметки, равного 0,9·n мм, можно записать 0,1·х = n – 0,9·n = =0,1·n, т.е. х = n. Следовательно, порядковый номер совпадающей отметки нониуса непосредственно дает число десятых долей миллиметра. На рисунке 3.4 n = 7 и 0,1·х = 0,7мм.