Алгоритм обработки при количестве наблюдений 40 заключается в следующем.
1 Группируют результаты наблюдений в порядке возрастания их значений: xmin–xmax .
2 Полученный диапазон результатов наблюдений разделяют на r одинаковых интервалов, равных 
.
3 Находят середины каждого интервала xjср и середину интервала с наибольшей частотой принимают за начало отсчета Х0 («ложный нуль»). Вычисляют для каждого интервала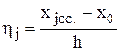 
.
4 Вычисляют точечные оценки первых двух начальных моментов сгруппированного распределения величины 
:
, 
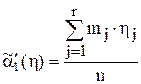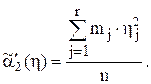
5 Находят точечную оценку второго центрального момента сгруппированного распределения величины :
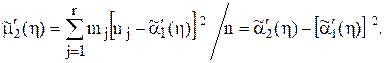
6 . Получим формулы, по которым вычисляют оцен-ки первого начального и второго центрального моментов результатов измерений: 
, 
.
7 Полученные оценки моментов неизбежно отличаются от моментов несгруппированного распределения, поскольку при группировании предполагается, что все частоты сконцентрированы в серединах интервалов. Для исправления оценок моментов результатов измерений можно принять: 
, 
.
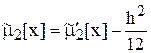8 Вычисляют точечные оценки математического ожидания измеряемой величины и с.к.о. результатов наблюдений: 
, 
.
9 Вычисляют случайные отклонения результатов наблюдений Vi . Используя критерий «трех сигм», определяют наличие грубых погрешностей и, если последние обнаружены, соответствующие результаты отбрасывают и повторяют вычисления в соответствии с п.1-8.
10 Вычисляют оценку с.к.о. результата измерения.
11 Используя критерий 
, проверяют нормальность распределения резуль-татов наблюдений.
12 По заданной доверительной вероятности Р определяют коэффициент Стьюдента (для Р=0,9 tp=1,645; для Р=0,95 tp=1,960; для Р=0,99 tp=2,576).
13 Рассчитываются доверительные границы случайной погрешности результата измерения.
Поможем написать любую работу на аналогичную тему