Обработка исправленных результатов прямых равнорассеянных наблюдений

Напомним, что исправленными результатами наблюдений называются результаты, не содержащие систематические погрешности измерений.

Исправленные результаты наблюдений x1,…,xn, полученные при прямых измерениях постоянной физической величины Qх, называются равнорассеянными (равноточными), если они являются независимыми, одинаково распределенными случайными величинами.

Равнорассеянные результаты получают при измерениях, проводимых одним наблюдателем или группой наблюдателей с помощью одних и тех же средств измерений в неизменных условиях внешней среды. Результаты обрабатывают по-разному в зависимости от того, мало (n40) или велико (n>40) количество наблюдений.

Алгоритм обработки при количестве наблюдений n40 заключается в следующем.

1 Определяют точечную оценку математического ожидания измеряемой величины – среднее арифметическое результатов наблюдений  по формуле 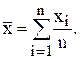   i = 1,…, n .                                                             Полученное числовое значение   округляют так , чтобы случайные отклонения результатов наблюдений имели не больше трех значащих цифр.

2 Вычисляют случайные отклонения результатов наблюдений Vi по формуле Vi = xi – .                                                                                                            Правильность расчетов  и Vi  может быть проверена путем суммирования всех случайных отклонений Vi+.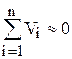                                             

 3 Определяют оценку c.к.о. результатов наблюдений х по формуле 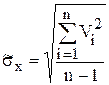.                                                                                                     (1.18)

4 Определяют наличие грубых погрешностей и, если последние обнаружены, соответствующие результаты отбрасывают и повторяют вычисления в соответствии с п. 1 – 3.

При количестве наблюдений n >30 наиболее часто используют критерий «трех сигм».

Более строгим является критерий, который заключается в проверке гипотезы, что результат наблюдения xi не будет содержать грубой погрешности, если он является одним из значений случайной величины x с нормальным законом распределения при количестве наблюдений n . Ф.Е. Граббсом были табулированы q-процентные точки распределения максимальных по модулю отклонений результатов наблюдений от их среднего значения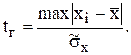    

>,   то такое наблюдение содержит грубую погрешность (для уровня значимости q) и должно быть исключено при обработке результатов наблюдений.

5 Определяют оценку с.к.о. результата измерения  по формуле        .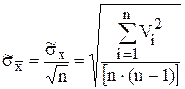                       

6 При помощи составного критерия производится  проверка нормальности распределения результатов наблюдений.

7 По заданной доверительной вероятности Р и числу наблюдений n определяется коэффициент Стьюдента tp.

8 Рассчитываются доверительные границы случайной погрешности результата измерения  .                                                       

Если сравнивать значения tp для разных распределений, то оказывается , что при Р>0,85 значение tp максимальны для нормального распределения. Поэтому при неизвестной функции распределения (или невозможности проверки принадлежности результатов наблюдений к нормальному распределению) рекомендуется распределение считать нормальным, так как надежность оценки  повышается.