Проверка нормальности распределения результатов наблюдений - Дисциплина метрология – шпаргалки к экзамену.

Сходимость результатов наблюдений можно оценить наиболее полно, если их распределение является нормальным. Поэтому исключительно важную роль при обработке результатов наблюдений играет проверка нормальности распределения.

Эта задача представляет собой частный случай более общей проблемы, заключающейся в подборе теоретической функции распределения, в некотором смысле наилучшим образом согласующейся с опытными данными.

При большом числе результатов наблюдений (n>40) данная задача решается в следующем порядке.

Группируют результаты наблюдений в порядке возрастания их значений: Xmin - Xmax. Весь диапазон результатов наблюдений разделяют на r интервалов шириной  DXj (j=1,…, r) и подсчитывают частоты mj, равные числу результатов, лежащих в каждом j-м интервале, т.е. меньших его правой и больших или равных левой границе.

Отношения Pj* =  mj/n ,           где n–общее число наблюдений, называются частостями и представляют собой статистические оценки вероятностей попадания результата наблюдений в j-й интервал. Распределение частостей по интервалам образует статистическое распределение результатов наблюдений.

Если теперь разделить частость на длину интервала, то получим величины pj*= Pj* / DXj  = mj / (n × DXj)            ,являющиеся оценками средней плотности распределения в интервале DXj .

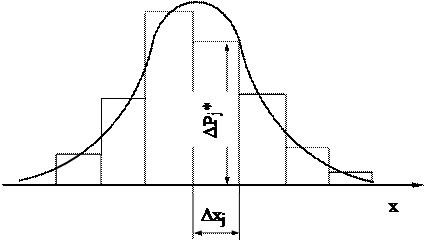
Если отложить вдоль оси результатов наблюдений интервалы DXj в порядке возрастания индекса j и на каждом интервале построить прямоугольник с высотой, равной pj*, то получим график, называемый гистограммой статистического распределения (рисунок 1.1). Площадь всех прямоугольников равна единице:

.

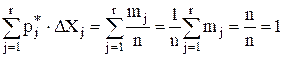Рисунок 1.1

При увеличении числа интервалов r гистограмма все больше приближается к плавной кривой, ограничивающей единичную площадь, - к графику дифференциальной функции распределения.

При построении гистограмм рекомендуется пользоваться следующими правилами:

- число r интервалов выбирается в зависимости от числа наблюдений n (при n=40-70  r=7-9; при n=100-500  r=8-12; при n=500-1000   r=10-16; при n=1000-10000    r=12-22);

- длины интервалов удобнее выбирать одинаковыми. Однако если распределение крайне неравномерно, то в области максимальной концентрации результатов наблюдений следует выбирать более узкие интервалы;

- масштабы по осям гистограммы должны быть такими, чтобы отношение ее высоты к основанию составляло примерно 5:8.

После построения гистограммы надо подобрать теоретическую плавную кривую распределения, которая, выражая все существенные черты статистического распределения, сглаживала бы все случайности, связанные с недостаточным объемом экспериментальных данных. Принципиальный вид теоретической кривой выбирают заранее, проанализировав метод измерения или хотя бы по внешнему виду гистограммы. Тогда определение аналитического вида кривой распределения сводится к выбору таких значений его параметров, при которых достигается наибольшее соответствие между теоретическим и статистическими распределениями.

Одним из методов решения этой задачи является метод моментов. При его использовании параметрам теоретического распределения придают такие значения, при которых несколько важнейших моментов совпадают с их статистическими оценками. Так, если статистическое распределение, определяемое  гистограммой, приведенной на рисунке 1.1, мы хотим описать кривой нормального распределения, то естественно потребовать, чтобы математическое ожидание и дисперсия последнего совпадали со средним арифметическим и оценкой дисперсии, вычисленным по опытным данным.

Далее законно возникает вопрос, объясняются ли расхождения между гистограммой и подобранным теоретическим распределением только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они вызваны тем, что результаты наблюдений в действительности распределены иначе.

Для ответа на этот вопрос используют методы проверки статистических гипотез. Идея их применения заключается в следующем. На основании гистограммы, полученной при обработке опытных данных, строится гипотеза, состоящая в том, что результаты наблюдений подчиняются распределению  F(x) с плотностью p(x).

Для того чтобы принять или опровергнуть эту гипотезу, выбирается некоторая величина U, представляющая собой меру расхождения теоретического и статистического распределений. В качестве меры расхождения можно принять сумму квадратов разностей частостей и теоретических вероятностей попадания результатов наблюдений в каждый интервал, взятых с некоторыми коэффициентами: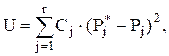где Cj – коэффициенты, называемые весами разрядов; Pj – теоретические вероятности, определяемые как 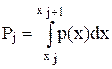.          Здесь  p(x) - предполагаемая плотность распределения.

Мера расхождения U является случайной величиной и, как показал К. Пирсон, независимо от исходного распределения подчиняется c2 – распределению c k степенями свободы. если все частоты mj5 и число измерений стремится к бесконечности, то веса Cj  выбираются равными n / Pj . Число степеней свободы распределения k = r – s, где r – число независимых связей, наложенных на частости Pj*.

Если проверяется гипотеза о нормальности распределения, то к числу этих связей относятся равенство среднего арифметического и точечной оценки дисперсии соответственно математическому ожиданию и дисперсии предполагаемого нормального распределения. Кроме того, всегда требуется, чтобы сумма частостей по всем интервалам была равна единице. Поэтому в данном случае s=3.

Мера расхождения U, выбранная по К. Пирсону, обозначается через c2k . Для удобства вычислений ее можно записать в ви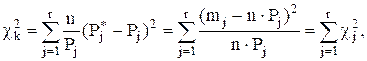де

     где 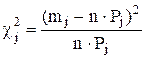 .                          Если вычисленная по опытным данным мера расхождения c2k окажется в указанном интервале, то гипотеза принимается. Это, конечно, не значит, что гипотеза верна. Можно лишь утверждать, что она правдоподобна, т.е. не противоречит опытным данным. Если же c2k выходит за границы доверительного интервала, то гипотеза отвергается как противоречащая опытным данным.

Поскольку проверка гипотезы основывается на опытных данных, то при принятии решения  всегда возможны ошибки. Отвергая в действительности верную гипотезу, мы совершаем ошибку первого рода. Вероятность ошибки первого рода называется уровнем значимости и составляет q = 1-a. Принимая в действительности неверную гипотезу, мы совершаем ошибку второго рода. Вычислить ее вероятность, вообще говоря, невозможно, поскольку для этого нужно рассмотреть все прочие возможные гипотезы, являющиеся альтернативой обсуждаемой гипотезы. Можно лишь утверждать, что при уменьшении ошибки первого рода ошибка второго рода увеличивается, поэтому не имеет смысла брать слишком высокие значения доверительных вероятностей.Описанная процедура проверки гипотезы о том, что данное статистическое распределение является распределением с плотностью p(x), называется критерием согласия c2.Проверка нормальности распределения согласно критерию c2 сводится к следующему:

1 Данные наблюдений группируют по интервалам, как при построении гистограммы, и подсчитывают частоты mj. Если в некоторые интервалы попадает меньше пяти наблюдений, то такие интервалы объединяют с соседними. При этом число степеней свободы k, конечно, уменьшается.

2 Вычисляют среднее арифметическое и точечную оценку среднего квадратического отклонения (с.к.о.) результатов наблюдений х, которые принимают в качестве параметров теоретического нормального распределения с плотностью p(x). Формулы для расчетов  и  х приведены в п. 1.2 настоящего учебного пособия.

3 Для каждого интервала находят вероятности попадания в них результатов наблюдений по формуле 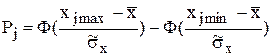  , где Ф(z) - интегральная функция нормированного нормального распре-деления; xjmax и xjmin- максимальное и минимальное значения х на j-м интервале.

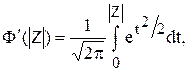 которая связана с интегральной функцией нормиро-ванного нормального распределения соотношением

             при этом     для   и      для   Z<0 .

4 Для каждого интервала вычисляют величины c2j (j =1,…, r) по формуле (1.6) и суммируют их по всем j по формуле (1.5), в результате чего получают меру расхождения c2k .

5 Определяют число степеней свободы k = r-3 и, задаваясь уровнем значимости q =1-a , находят c2k;q/2 и c2k;1-q .

Если  c2k;q/2c2kc2k;1-q/2 , то распределение результатов считают нормальным.

При 10 < n  50 для проверки нормальности распределения используется составной критерий , который заключается в следующем.

Критерий 1. Исходя из результатов наблюдений X1,…,Xn вычисляем значение параметра d по формул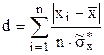е   ,  где    .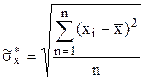                                                                                       

Выбирается уровень значимости q и исходя из значений q и n находятся значения точек распределения (1.10) dn;q/2 и dn;1-q/2, приведенные в таблице В.1. Считается, что гипотеза о нормальности по критерию 1 не отвергается, если dn;1- q/2 d dn; q/2 .        В противном случае гипотеза отвергается.

Критерий 2. Принимается, что гипотеза о нормальности по критерию 2 не отвергается, если не более m разностей  превзошли , где Z – аргумент интегральной функции нормированного нормального распределения Ф(Z). Значение Z находится из таблицы Г.1, исходя из значения Ф(Z), равного доверительной вероятности . Значение определяется по n и уровню значимости q как корень уравнения 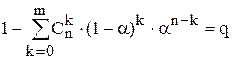.                При 10 £ n £ 20 следует принимать m=1. Если 20 < n £ 50, то m=2. Если число разностей   больших , превышает m, то гипотеза о нормальности отвергается.

Гипотеза о нормальности принимается, если для проверяемой группы результатов наблюдений выполняются оба критерия. Уровень значимости составного критерия  где q1 и q2 – уровень значимости для критериев 1 и 2 соответственно.

45. Понятие о средстве измерений

Понятие «средство измерений» является одним из важнейших в теоретической метрологии. ГОСТ 16263-70 определяет средство измерений (СИ) как техническое средство, используемое при измерениях и имеющее нормированные метрологические свойства.

СИ является обобщённым понятием, объединяющим самые разнообразные конструктивно законченные устройства, которые реализуют одну из двух функций:

воспроизводят величину заданного (известного) размера - например, гиря - заданную массу, магазин сопротивлений - ряд дискретных значений сопротивления;

вырабатывают сигнал (показание), несущий информацию о значении измеряемой величины. Показания СИ либо непосредственно воспринимаются органами чувств человека (например, показания стрелочного или цифрового приборов), либо они недоступны восприятию человеком и используются для преобразования другими СИ.

   СИ содержат устройства, которые выполняют элементарные измерительные операции. В их число входят измерительные преобразователи (ИП), меры и устройства сравнения (УС), иначе называемые компараторами.

   Измерительный преобразователь - это СИ, построенное на определенном физическом принципе и выполняющее одно частное измерительное преобразование, т.е. операцию преобразования входного сигнала Х в выходной Х1, информативный параметр которого с заданной степенью точности функционально связан с информативным параметром входного сигнала и может быть измерен с достаточной степенью точности. Информативным параметром входного сигнала СИ является параметр входного сигнала, функционально связанный с измеряемой величиной и используемый для передачи ее значения или являющийся самой измеряемой величиной.

   Мера - это СИ, предназначенное для воспроизведения и (или) хранения физической величины одного (однозначная мера) или нескольких (многозначная мера) размеров, значения которых выражены в установленных единицах и известны с необходимой точностью.

   Устройство сравнения (компаратор) - это техническое средство измерений, дающее возможность выполнять сравнение мер однородных величин или же показаний измерительных приборов.

   Обобщённая структурная схема СИ показана на рисунке 1.1. Входным сигналом является измерительный сигнал, один из параметров которого однозначно связан с измеряемой величиной: , где а0 - информативный параметр входного сигнала; y(t) - измеряемая величина; а1, а2, …,аn - неинформативные параметры входного сигнала. Неинформативным параметром входного сигнала СИ называется его параметр, не используемый для передачи значения измеряемой величины.

   Входной сигнал преобразуется измерительным преобразователем в пропорциональный ему сигнал X1. Следует отметить, что преобразователь может отсутствовать, тогда входной сигнал будет подаваться непосредственно на один из входов устройства сравнения. Однако в большинстве случаев он входит в состав СИ.

   Сравнение измеряемой и известной величин осуществляется при помощи устройства сравнения. Роль последнего в простейших СИ, имеющих отсчетные шкалы, выполняет человек. Например, при измерении длины тела он сопоставляет её с многозначной мерой - линейкой и находит количество N квантов меры, равное с точностью до кванта измеряемой длине.

УС даёт информацию о том, какое значение выходного сигнала многозначной меры должно быть установлено автоматически или при участии оператора. Процесс изменения прекращается при достижении равенства между величинами X1 и XM с точностью до кванта .

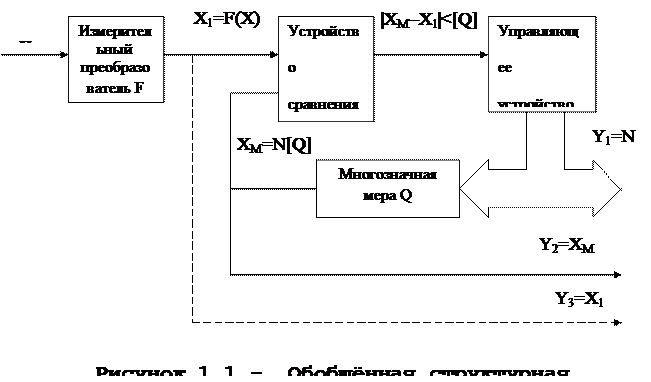   Выходным сигналом может служить один из трёх сигналов: Y1, Y2, Y3. Если выходной сигнал предназначен для непосредственного восприятия человеком, то его роль выполняет сигнал Y1=N. В данном случае код N является привычным для человека десятичным кодом.

   Если же выходной сигнал СИ предназначен для применения в других СИ, то в качестве него может быть использован любой из трёх сигналов: Y1, Y2  и Y3. Первый из них при этом является цифровым, как правило, двоичным кодом, который «понимают» входные цифровые устройства последующих СИ. Аналоговый сигнал Y2 квантован по уровню и представляет собой эквивалент цифрового кода N, а СИ в этом случае предназначено для воспроизведения физической величины заданного размера и состоит только из одного блока - многозначной меры. Сигнал Y3 представляет собой измерительное преобразование входного сигнала X, СИ при этом используется только как ИП, а остальные его блоки отсутствуют.

   Таким образом, структурная схема, показанная на рисунке 1.1, описывает три возможных варианта:

СИ включает все блоки и вырабатывает сигнал Y1, доступный восприятию органами чувств человека. Возможно формирование выходных сигналов Y1 и Y2, предназначенных только для преобразования другими СИ;

СИ состоит только из ИП, выходной сигнал которого равен Y3;

СИ содержит только меру, выходной сигнал которой равен Y2.

   В общем случае выходной сигнал Y(X) описывается выражением Y=Y{b0, b1, b2 …, bm, S1, S2, …, Sl, x1, x2, …, xk}, где b0 - информативный параметр выходного сигнала, функционально связанный с информативным параметром входного сигнала; b1, b2, …, bm - неинформативные параметры выходного сигнала; S1, S2, …, Sl - параметры СИ, зависящие от его методической и аппаратной реализации; x1, x2, …, xk - влияющие величины. Неинформативным параметром выходного сигнала СИ называется параметр, не используемый для передачи или индикации значения информативного параметра входного сигнала.

   СИ могут работать в двух режимах: статическом и динамическом. Статитический режим - это такой режим работы СИ, при котором изменением измеряемой величины за время, требуемое для проведения одного измерения, можно пренебречь. В динамическом режиме такое пренебрежение недопустимо, поскольку указанное изменение превышает допустимую погрешность.