В статических режимах выходной сигнал СИ в точности соответствует входному (при условии отсутствия статических погрешностей) и, следовательно, коэффициент преобразования К равен номинальному коэффициенту К0 во всем диапазоне изменения входной величины X(t). Уравнение преобразования имеет вид 
и соответствует идеальному безынерционному линейному преобразованию. Реальные СИ обладают инерционными (динамическими) свойствами, обусловленными особенностями используемых элементов. Это приводит к более сложной зависимости между входным и выходным сигналами. Свойства СИ в динамических режимах, т.е. когда время изменения измеряемой величины сравнимо со временем измерения, описываются совокупностью так называемых динамических характеристик.
Основной их них является полная динамическая характеристика, полностью описывающая принятую математическую модель динамических свойств СИ. В качестве нее используют: дифференциальные уравнения; переходную, импульсную переходную, амплитудно-фазовую и амплитудно-частотную характеристики; совокупность амплитудно-частотной и фазочастотной характеристик; передаточную функцию.
Дифференциальные уравнения наиболее полно описывают динамические свойства СИ. Общий вид уравнения: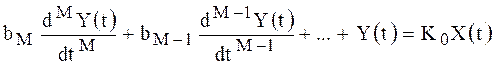 
где bM, bM–1, … - постоянные коэффициенты.
Его решение Y(t) описывает выходной сигнал средства измерений при входном сигнале X(t).
Переходная характеристика h(t) - это временная характеристика СИ, полученная в результате подачи на его вход сигнала в виде единичной функции заданной амплитуды X(t) = ХM×1(t). Она описывает инерционность СИ, обуславливающую запаздывание и искажение выходного сигнала относительно входного. Переходную характеристику находят либо опытным путем, либо решая соответствующее дифференциальное уравнение при X(t) =ХМ×1(t).
Импульсная переходная характеристика g(t) - это временная характеристика СИ, полученная в результате приложении к его входу сигнала в виде дельта-функции.
Поможем написать любую работу на аналогичную тему