Как и дифференциальное уравнение, эти характеристики в полной мере определяют динамические свойства СИ. Выходной сигнал при известном входном X(t) определяют с помощью интеграла Дюамеля: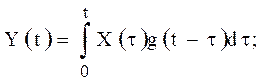 
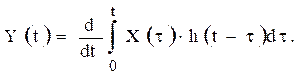
К частотным характеристикам относятся амплитудно-фазовая G(jw), амплитудно-частотная А(w) и фазочастотная j(w) характеристики. Частотные методы анализа основаны на исследовании прохождения гармонических колебаний различных частот через СИ. Если на вход линейного СИ подать входной сигнал 
то выходной сигнал можно записать в виде 
.
Амплитудно–фазовой характеристикой называют отношение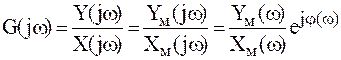 
.
Она описывает изменение показаний СИ при изменении частоты входного сигнала и характеризует только установившийся режим работы.
В практике измерений получила большое распространение амплитудно–частотная характеристика (АЧХ) 
,
представляющая собой зависящее от круговой частоты отношение амплитуды выходного сигнала линейного СИ в установившемся режиме к амплитуде входного синусоидального сигнала.
Фазочастотная характеристика (ФЧХ) j(w) - это зависящая от частоты разность фаз между выходным сигналом и входным синусоидальным сигналом линейного СИ в установившемся режиме.
Ясная физическая интерпретация и относительная простота экспериментального определения послужили причиной широкого применения частотных характеристик в метрологии.
Частотные характеристики СИ связаны с другими его динамическими характеристиками следующими соотношениями:
; 
.
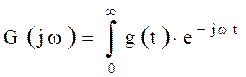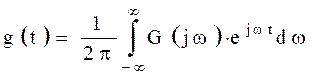Поможем написать любую работу на аналогичную тему