Классы точности средств измерений - Дисциплина метрология – шпаргалки к экзамену.

            Характеристики, введенные ГОСТ 8.009-84, наиболее полно описывают метрологические свойства СИ. Однако в настоящее время в эксплуатации находится достаточно большое число СИ, метрологические характеристики которых нормированы несколько по-другому, а именно на основе классов точности. Класс точности  - это обобщенная характеристика СИ, выражаемая пределами допускаемых значений его основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность. Класс точности не является непосредственной оценкой точности измерений, выполняемых этим СИ, поскольку погрешность зависит еще от ряда факторов: метода измерений, условий измерений и т.д. Класс точности лишь позволяет судить о том, в каких пределах находится погрешность СИ данного типа. Общие положения деления средств измерений по классу точности устанавливает ГОСТ 8.401-80.

            Пределы допускаемой основной погрешности  определяемые классом точности - это интервал, в котором находится значение основной погрешности СИ. Если СИ имеет незначительную случайную составляющую, то определение  относится к нахождению систематической погрешности и случайной погрешности, обусловленной гистерезисом, и является достаточно строгим. При этом предел .

            Если СИ имеет существенную случайную погрешность, то для него определение предела допускаемой основной погрешности является нечетким. Его следует понимать как интервал, в котором находится значение основной погрешности с неизвестной вероятностью, близкой к единице: , где К - коэффициент, зависящий от доверительной вероятности Р.

                        Классы точности СИ устанавливаются в стандартах или технических условиях. Средство измерений может иметь два и более класса точности. Например, при наличии у него двух или более диапазонов измерений одной и той же физической величины ему можно присваивать два или более класса точности. При-боры, предназначенные для измерения нескольких физических величин, так-же могут иметь различные классы точности для каждой измеряемой величины.

            Пределы допускаемых основной и дополнительной погрешностей выражают в форме приведенных, относительных или абсолютных погрешностей. Выбор формы представления зависит от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения СИ.

            Пределы допускаемой абсолютной основной погрешности устанавливаются по одной из формул: ∆=±а  или  ∆= ±(а + bх), где х - значение измеряемой величины или число делений, отсчитанное по шкале; а, b - положительные числа, не зависящие от х. Первая формула описывает чисто аддитивную погрешность (рисунок 2.4,а), а вторая - сумму аддитивной и мультипликативной погрешностей (рисунок  2.4,в). В технической документации классы точности, установленные в виде абсолютных погрешностей, обозначают, например, «Класс точности М», а на приборе - буквой «М». Для обозначения используются прописные буквы латинского алфавита или римские цифры, причем меньшие пределы погрешностей должны соответствовать буквам, находящимся ближе к началу алфавита, или меньшим цифрам.

            Пределы допускаемой приведенной основной погрешности определяются по формуле   , где ХN - нормирующее значение, выраженное в тех же единицах, что и ∆; р - отвлеченное положительное число, выбираемое из ряда значений: (1; 1,5; 2; 2,5; 4; 5; 6)×10n; n=l; 0; -1; -2;...

Нормирующее значение XN устанавливается равным большему из пределов измерений (или модулей) для СИ с равномерной, практически равномерной или степенной шкалами и для измерительных преобразователей, если нулевое значение выходного сигнала находится на краю или вне диапазона измерений.

            Для СИ, нуль которых расположен внутри шкалы, XN равно модулю разности пределов измерений. Например, для вольтметра термоэлектрического термометра с пределами измерений -100 и 600°С нормирующее значение равно 700°С. Для СИ с заданным номинальным значением XN устанавливают равным этому значению. Для приборов с существенно неравномерной шкалой XN,. принимают равным всей длине шкалы или ее части, соответствующей диапазону измерений. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах длины, а на средстве измерений класс точности условно обозначают, например, в виде значка       , где 0,5 - значение числа р. В остальных рассмотренных случаях класс точности обозначают конкретным числом р, например 1,5. Обозначение наносится на циферблат, щиток или корпус прибора. Пределы допускаемой относительной основной погрешности определяются по формуле , если ∆=±а. Значение постоянного числа q устанавливается так же, как и значение числа р. Класс точности на прибор обозначается в виде, где 0,5 - конкретное значение q.

            В случае, если абсолютная погрешность задается формулой ±(а+bх), пределы допускаемой относительной основной погрешности  ,       где с, d — отвлеченные положительные числа, выбираемые из ряда:(1; 1,5; 2; 2.5; 4; 5; 6)×10n; n=1; 0; -1; -2 и т.д.; XK - больший (по модулю) из пределов измерений. При использовании формулы (2.4) класс точности обозначается в виде «0,02/0,01», где числитель - конкретное значение числа с, знаменатель - числа d. В обоснованных случаях пределы допускаемой относительной основной погрешности определяют по более сложным формулам либо в виде графика или таблицы.

            В стандартах или технических условиях на СИ указывается минимальное значение X0 , начиная с которого применим принятый способ выражения пределов допускаемой относительной погрешности. Отношение Xк/Х0 называется динамическим диапазоном измерения.

            Предел допускаемой дополнительной погрешности может указываться в виде:

            - постоянного значения для всей рабочей области влияющей величины или постоянных значений по интервалам рабочей области влияющей величины;

            - отношения предела допускаемой дополнительной погрешности, соответствующего регламентированному интервалу влияющей величины, к этому интервалу;

            - зависимости предела ∆дси  от влияющей величины (предельной функции влияния);

            - функциональной зависимости пределов допускаемых отклонений от номинальной функции влияния.

В 1993 г. под эгидой Международного комитета мер и весов (МКМВ), Международной электротехнической комиссии (МЭК), Международной организации по стандартизации (ИСО), Международной организации по законодательной метрологии (МОЗМ), Международного союза по чистой и прикладной физике, Международного союза по чистой и прикладной химии и Международной федерации клинической химии разработано "Руководство по выражению неопределенности измерения" (далее - Руководство).

Целями Руководства являются:

- обеспечение полной информации о том, как составлять отчеты о неопределенностях измерений;

- предоставление основы для международного сопоставления результатов измерений;

- предоставление универсального метода для выражения и оценивания неопределенности измерений, применимого ко всем видам измерений и всем типам данных, которые используются при измерениях.

Существуют два подхода к оцениванию параметров (характеристик) точности измерений. Один подход основан на понятиях и терминах, используемых в Руководстве, другой - на понятиях и терминах, применяемых в основополагающих нормативных документах (НД) в области метрологии, используемых в национальных системах обеспечения единства измерений государств - участников Соглашения "О проведении согласованной политики в области стандартизации, метрологии и сертификации" (далее - Соглашение).

Задачами настоящих рекомендаций являются:

- изложение основных положений Руководства и рекомендаций по их практическому применению;

- сравнительный анализ двух подходов к описанию точности измерений;

- показ соответствия между формами представления результатов измерений, используемыми в основополагающих НД в области метрологии, и формой, используемой в Руководстве.

1 Область применения

Настоящие рекомендации распространяются на методы оценивания точности результатов измерений, содержат практические рекомендации по применению Руководства и показывают соответствие между формами представления результатов измерений, принятыми в основополагающих нормативных документах (НД) по метрологии, применяемых в странах - участниках Соглашения, и формой, принятой в Руководстве.

3 Определения и обозначения

3.1 В настоящих рекомендациях использованы следующие основные термины, определенные в Руководстве:

неопределенность (измерений): Параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые могли бы быть обоснованно приписаны измеряемой величине;

стандартная неопределенность (u): Неопределенность результата измерений, выраженная в виде среднего квадратического отклонения (СКО);

суммарная стандартная неопределенность (uc): Стандартная неопределенность результата измерений, полученного через значения других величин, равная положительному квадратному корню суммы членов, причем члены являются дисперсиями или ковариациями этих других величин, взвешенными в соответствии с тем, как результат измерений изменяется при изменении этих величин;

расширенная неопределенность (U): Величина, определяющая интервал вокруг результата измерений, в пределах которого, как можно ожидать, находится большая часть распределения значений, которые с достаточным основанием могли бы быть приписаны измеряемой величине.

3.2 В настоящих рекомендациях использованы следующие обозначения:

xi - оценка i-й входной величины;

xil - l-й результат измерения i-й входной величины;

 - среднее арифметическое значение i-й входной величины;

y - оценка измеряемой величины;

u - стандартная неопределенность;

 - стандартная неопределенность, оцененная по типу А;

 - стандартная неопределенность, оцененная по типу B;

 - стандартная неопределенность оценки i -й входной величины;

 - стандартная неопределенность единичного измерения i-й входной величины;

 - коэффициент корреляции оценок i-й и j-й входных величин;

 - суммарная стандартная неопределенность;

k - коэффициент охвата;

 - квантиль распределения Стьюдента для доверительной вероятности (уровня доверия) p и числа степеней свободы v;

 - число степеней свободы при вычислении неопределенности оценки i-й входной величины;

- эффективное число степеней свободы, принятое в Руководстве;

- оценка эффективного числа степеней свободы;

U - расширенная неопределенность;

 - расширенная неопределенность для уровня доверия p;

S - СКО случайной погрешности результата измерений;

 - СКО единичного измерения при многократных измерениях i-й входной величины;

 - СКО среднего арифметического значения при многократных измерениях i-й входной величины;

SS - СКО суммы случайных и неисключенных систематических погрешностей;

K - коэффициент при суммировании систематической и случайной составляющих суммарной погрешности, принятый в НД ГСИ по метрологии*;

fэф - оценка эффективного числа степеней свободы, принятая в НД ГСИ по метрологии;

Dp - доверительные границы суммарной погрешности результата измерений для доверительной вероятности p;

zp - квантиль нормального распределения для доверительной вероятности p;

qi - границы i-й составляющей неисключенной систематической погрешности;

q(p) - доверительные границы систематической погрешности измерения для доверительной вероятности p;

bi- - нижняя граница отклонения измеряемой величины от результата измерений;

bi+ - верхняя граница отклонения измеряемой величины от результата измерений;

bi - симметричные границы отклонения измеряемой величины от результата измерений.

4 Рекомендации по применению Руководства

4.1 Основным количественным выражением неопределенности измерений является стандартная неопределенность u.

4.2 Основным количественным выражением неопределенности измерений, при котором результат определяют через значения других величин, является суммарная стандартная неопределенность .

4.3 В тех случаях, когда это необходимо, вычисляют расширенную неопределенность U по формуле

                                                                   (1)

где k - коэффициент охвата (числовой коэффициент, используемый как множитель при суммарной стандартной неопределенности для получения расширенной неопределенности).

4.4 В Руководстве измеряемую величину Y определяют как

,                                                             (2)

где  - входные величины (непосредственно измеряемые или другие величины, влияющие на результат измерения);

m - число этих величин;

f - вид функциональной зависимости.

4.5 Оценку измеряемой величины y вычисляют как функцию оценок входных величин  после внесения поправок на все известные источники неопределенности, имеющие систематический характер

.                                                             (3)

4.6 Затем вычисляют стандартные неопределенности входных величин  и возможные коэффициенты корреляции  оценок i-й и j-й входных величин .

4.7 Различают два типа вычисления стандартной неопределенности:

вычисление по типу А - путем статистического анализа результатов многократных измерений;

вычисление по типу В - с использованием других способов.

4.8.1 Вычисление стандартной неопределенности по типу А -

4.8.1.1 Исходными данными для вычисления  являются результаты многократных измерений: xi1, …,  (где i = 1, …; m;  - число измерений i-й входной величины).

4.8.1.2 Стандартную неопределенность единичного измерения i-й входной величины  вычисляют по формуле

,                                                       (4)

где  - среднее арифметическое результатов измерений i-й входной величины.

4.8.1.3 Стандартную неопределенность  измерений i-й входной величины, при которых результат определяют как среднее арифметическое, вычисляют по формуле

.                                              (5)

4.8.2 Вычисление стандартной неопределенности по типу В –

4.8.2.1 В качестве исходных данных для вычисления  используют:

- данные предшествовавших измерений величин, входящих в уравнение измерения; сведения о виде распределения вероятностей;

- данные, основанные на опыте исследователя или общих знаниях о поведении и свойствах соответствующих приборов и материалов;

- неопределенности констант и справочных данных;

- данные поверки, калибровки, сведения изготовителя о приборе и т.п.

4.8.2.2 Неопределенности этих данных обычно представляют в виде границ отклонения значения величины от ее оценки. Наиболее распространенный способ формализации неполного знания о значении величины заключается в постулировании равномерного закона распределения возможных значений этой величины в указанных (нижней и верхней) границах . При этом стандартную неопределенность, вычисляемую по типу В - , определяют по формуле

,                                                           (6)

а для симметричных границ  - по формуле

.                                                                (7)

4.8.2.3 В случае других законов распределения формулы для вычисления неопределенности по типу В будут иными.

4.8.3 Для вычисления коэффициента корреляции  используют согласованные пары измерений  (где l = 1; …,  - число согласованных пар результатов измерений)

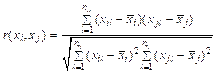.                                              (8)

4.9 Вычисление суммарной стандартной неопределенности

4.9.1 В случае некоррелированных оценок , суммарную стандартную неопределенность  вычисляют по формуле

.                                                       (9)

4.9.2 В случае коррелированных оценок  суммарную стандартную неопределенность вычисляют по формуле

,                      (10)

где  - коэффициент корреляции;

- стандартная неопределенность i -й входной величины, вычисленная по типу А или В.

4.10 Выбор коэффициента охвата k при вычислении расширенной неопределенности

4.10.1 В общем случае коэффициент охвата k выбирают в соответствии с формулой

,                                                            (11)

где  - квантиль распределения Стьюдента с эффективным числом степеней свободы  и доверительной вероятностью (уровнем доверия) p. Значения коэффициента  приведены в приложении Г.

4.10.2 Эффективное число степеней свободы определяют по формуле

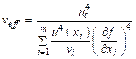,                                                       (12)

где  - число степеней свободы при определении оценки i-й входной величины, при этом:

 - для вычисления неопределенностей по типу А;

 - для вычисления неопределенностей по типу В.

4.10.3 Во многих практических случаях при вычислении неопределенностей результатов измерений делают предположение о нормальности закона распределения возможных значений измеряемой величины и полагают:

k = 2 при  и k = 3 при .

При предположении о равномерности закона распределения полагают:

k = 1,65 при  и k = 1,71 при.