Релятивистская (эйнштейновская) механика

Долгое время казалось, что механика Ньютона может дать теоретическое объяснение любых явлений. Однако постепенно выявлялись границы применимости классической механики. Решающую роль сыграло здесь изучение электромагнитных процессов и создание классической теории электромагнетизма. Центральное место в этой теории занимает представление об электромагнитном поле. Электромагнитное поле - особый вид материи, который подчиняется не законам классической механики (механики Ньютона), а иным законам, математическим выражением которых являются уравнения Максвелла.

Теории электромагнитного поля Максвелла были присущи два недостатка:

1. Она не совмещалась с принципом относительности движения классической физики, поскольку ее уравнения оказались неинвариантными относительно преобразований Галилея.

2. Полевая картина физической реальности оказалась теоретически неполной и логически противоречивой. Эйнштейн отмечал: теория Максвелла хотя и правильно описывает поведение электрически заряженных частиц ,но не дает теории этих частиц. Следовательно, они должны рассматриваться на основе классической механики как материальные точки, расположенные в пространстве дискретно, что противоречит понятию поля. Последовательная полевая теория требует непрерывности всех элементов теории.

Объектом изучения в классической механике были или материальные точки, или точки пространства, или моменты времени. Эйнштейн отвергает все эти разделительные «или».

Объектом теории относительности выступают «физические события» как целостные объекты, в которых объединены понятия материи, движения, пространства, времени.

Физической реальностью обладают только сами события, определенные четырьмя числами x, y, z, t. «Законы природы примут наиболее удовлетворительный вид, будучи выражены как законы в четырехмерном пространственно- временном континууме».

Остановимся теперь на первом недостатке. Анализ показал, что уравнения Максвелла неинвариантны относительно галилеевых преобразований.  Это значит, что при переходе от одной ИСО к другой форма уравнений оказалась разной. Это равносильно тому, что в разных системах отсчета один и тот же физический процесс осуществлялся по разным законам, что противоречит науке.

Проблему пытались решить путем переработки уравнений Максвелла, это ни к чему не привело.

В 1904 г. Лоренц решил видоизменить правила галилеевых преобразований так, чтобы относительно этих правил уравнения Максвелла оказались инвариантными.

Лоренцевы преобразования – это новые правила перехода от одной ИСО к другой. Для случая, когда система K' движется относительно K со скоростью υ вдоль оси x, преобразования Лоренца имеют вид:

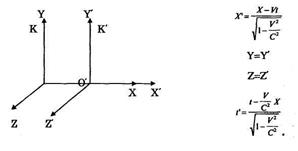
Лоренц искусственно получил новые правила перехода. При этом уравнения Максвелла оказываются инвариантными в любых ИСО. Однако неясно  было имеют ли преобразования физический смысл.

Эйнштейн предпринял попытку дедуктивного построения теории, которая бы наполнила преобразования Лоренца физическим смыслом – теорию относительности.

Теория относительности Эйнштейна объединяет классическую механику и электромагнитную теорию Максвелла и выступает как релятивистская механика.

Релятивистская (эйнштейновская) механика изучает движение материальных объектов при скоростях, сравнимых со скоростью света в вакууме.

В ее основе лежат два постулата:

1. Принцип относительности движения. Равноправие всех инерциальных систем отсчета. Инерциальная система отсчета – это система отсчета, в которой справедлив первый закон Ньютона (закон инерции). Любая система отсчета, движущаяся относительно инерциальной системы отсчета поступательно, равномерно и прямолинейно, также является инерциальной системой отсчета. Напомним, что движение тела, при котором все его точки в данный момент времени движутся одинаково, называется поступательным движением. Движение с постоянной по модулю и направлению скоростью называется равномерным прямолинейным движением. При равномерном прямолинейном движении тело движется по прямой и за любые равные промежутки времени проходит одинаковый путь.

Равноправие всех инерциальных систем отсчета означает, что во всех таких системах законы физики одинаковы. Это утверждение называется релятивистской инвариантностью.

2. Принцип постоянства скорости света в вакууме. Скорость света в вакууме принято обозначать буквой с (с= 300000 км/с). Этот постулат означает, что скорость света в вакууме не зависит от движения источника света.

Скорость света является максимальной возможной скоростью распространения материальных взаимодействий.

Первый постулат означает, что, находясь в закрытой кабине и производя наблюдения над механическим движением, электрическими и магнитными процессами и любыми другими явлениями, невозможно установить, покоится кабина или движется равномерно и прямолинейно. Тем самым устанавливается относительность понятий “покой” и “равномерное прямолинейное движение”.

Из этих двух физических принципов Эйнштейн заново вывел математические преобразования Лоренца, но теперь наполнив их физическим смыслом.

Релятивистские эффекты:

1. с ростом механической скорости объекта, его пространственные размеры укорачиваются:

где l  -длина объекта, движущегося со скоростью v;

l0 - длина объекта при v = 0;

c - скорость света в вакууме.

2.  с ростом механической скорости объекта время протекания процессов замедляется по формуле:

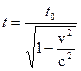
3. с ростом механической скорости объекта масса объекта увеличивается по формуле:

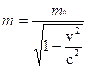
При выполнении любых физических измерений исключительную роль играют пространственно-временные соотношения между событиями. В СТО событие определяется как физическое явление, происходящее в какой-либо точке пространства в некоторый момент времени в избранной системе отсчета. Таким образом, чтобы полностью охарактеризовать событие, требуется не только выяснить его физическое содержание, но и определить его место и время. Для этого необходимо использовать процедуры измерения расстояний и промежутков времени. Эйнштейн показал, что эти процедуры нуждаются в строгом определении.

Для того чтобы в выбранной системе отсчета выполнять измерения промежутка времени между двумя событиями (например, началом и концом какого-либо процесса), происходящими в одной и той же точке пространства, достаточно иметь эталонные часы. Наибольшей точностью в настоящее время обладают часы, основанные на использовании собственных колебаний молекул аммиака (молекулярные часы) или атомов цезия (атомные часы). Измерение промежутка времени опирается на понятие одновременности: длительность какого-либо процесса определяется путем сравнения с промежутком времени, отделяющим показание часов, одновременное с концом процесса, от показания тех же часов, одновременного с началом процесса. Если же оба события происходят в разных точках системы отсчета, то для измерения промежутков времени между ними в этих точках необходимо иметь синхронизованные часы.

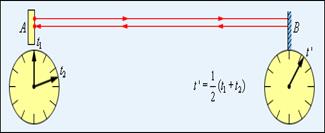
Эйнштейновское определение процедуры синхронизации часов основано на независимости скорости света в пустоте от направления распространения. Пусть из точки A в момент времени t1 по часам A отправляется короткий световой импульс (рис. 1). Пусть время прихода импульса в B и отражения его назад на часах B есть t'. Наконец, пусть отраженный сигнал возвращается в A в момент t2 по часам A. Тогда по определению часы в A и B идут синхронно, если t' = (t1 + t2) / 2.

1

Рисунок 1. Синхронизация часов в СТО.

Существование единого мирового времени, не зависящего от системы отсчета, которое принималось как очевидный факт в классической физике, эквивалентно неявному допущению о возможности синхронизации часов с помощью сигнала, распространяющегося с бесконечно большой скоростью.

Итак, в разных точках выбранной системы отсчета можно расположить синхронизованные часы. Теперь можно дать определение понятия одновременности событий, происходящих в пространственно-разобщенных точках: эти события одновременны, если синхронизованные часы показывают одинаковое время.

Рассмотрим теперь вторую инерциальную систему K', которая движется с некоторой скоростью υ в положительном направлении оси x системы K. В разных точках этой новой системы отсчета также можно расположить часы и синхронизировать их между собой, используя описанную выше процедуру. Теперь интервал времени между двумя событиями можно измерять как по часам в системе K, так и по часам в системе K'. Будут ли эти интервалы одинаковы? Ответ на этот вопрос должен находиться в согласии с постулатами СТО.

Пусть оба события в системе K' происходят в одной и той же точке и промежуток времени между ними равен τ0 по часам системы K'. Этот промежуток времени называется собственным временем. Каким будет промежуток времени между этими же событиями, если его измерить по часам системы K?

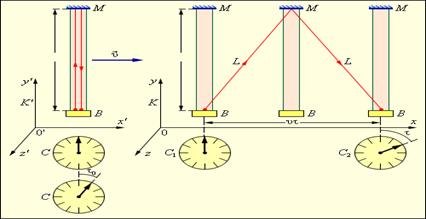
Для ответа на этот вопрос рассмотрим следующий мысленный эксперимент. На одном конце твердого стержня некоторой длины l расположена импульсная лампа B, а на другом конце – отражающее зеркало M. Стержень расположен, неподвижно в системе K' и ориентирован параллельно оси y' (рис. 2). Событие 1 – вспышка лампы, событие 2 – возвращение короткого светового импульса к лампе.

В системе K' оба рассматриваемых события происходят в одной и той же точке. Промежуток времени между ними (собственное время) равен τ = 2l / c. С точки зрения наблюдателя, находящегося в системе K, световой импульс движется между зеркалами зигзагообразно и проходит путь 2L, равный

где τ – промежуток времени между отправлением светового импульса и его возвращением, измеренный по синхронизованным часам C1 и C2, расположенными в разных точках системы K.

2

Рисунок 2. Относительность промежутков времени. Моменты наступлений событий в системе K' фиксируются по одним и тем же часам C, а в системе K – по двум синхронизованным пространственно-разнесенным часам C1 и C2. Система K' движется со скоростью υ в положительном направлении оси x системы K.

Но согласно второму постулату СТО, световой импульс двигался в системе K с той же скоростью c, что и в системе K'. Следовательно, τ = 2L / c. 

Из этих соотношений можно найти связь между τ и τ0:

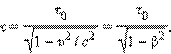
где β = υ / c.

Таким образом, промежуток времени между двумя событиями зависит от системы отсчета, то есть является относительным. Собственное время τ0 всегда меньше, чем промежуток времени между этими же событиями, измеренный в любой другой системе отсчета. Этот эффект называют релятивистским замедлением времени. Замедление времени является следствием инвариантности скорости света.

Эффект замедления времени является взаимным, в согласии с постулатом о равноправии инерциальных систем K и K': для любого наблюдателя в K или K' медленнее идут часы, связанные с движущейся по отношению к наблюдателю системой. Этот вывод СТО находит непосредственное опытное подтверждение. Например, при исследовании космических лучей в их составе обнаружены μ-мезоны – элементарные частицы с массой, примерно в 200 раз превышающей массу электрона. Эти частицы нестабильны, их среднее собственное время жизни равно τ0 = 2,2·10–6 с. Но в космических лучах μ-мезоны движутся со скоростью, близкой к скорости света. Без учета релятивистского эффекта замедления времени они в среднем пролетали бы в атмосфере путь, равный cτ0 ≈ 660 м. На самом деле, как показывает опыт, мезоны за время жизни успевают пролетать без распада гораздо большие расстояния. Согласно СТО, среднее время жизни мезонов по часам земного наблюдателя равно 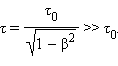, так как β = υ / c близко к единице. Поэтому средний путь υτ, проходимый мезоном в земной системе отсчета, оказывается значительно больше 660 м.

С релятивистским эффектом замедления времени связан так называемый «парадокс близнецов». Предполагается, что один из близнецов остается на Земле, а второй отправляется в длительное космическое путешествие с субсветовой скоростью. С точки зрения земного наблюдателя, время в космическом корабле течет медленнее, и когда астронавт возвратится на Землю, он окажется гораздо моложе своего брата-близнеца, оставшегося на Земле. Парадокс заключается в том, что подобное заключение может сделать и второй из близнецов, отправляющийся в космическое путешествие. Для него медленнее течет время на Земле, и он может ожидать, что по возвращению после длительного путешествия на Землю он обнаружит, что его брат-близнец, оставшийся на Земле, гораздо моложе его.

Чтобы разрешить «парадокс близнецов», следует принять во внимание неравноправие систем отсчета, в которых находятся оба брата-близнеца. Первый из них, оставшийся на Земле, все время находится в инерциальной системе отсчета, тогда как система отсчета, связанная с космическим кораблем, принципиально неинерциальная. Космический корабль испытывает ускорения при разгоне во время старта, при изменении направления движения в дальней точке траектории и при торможении перед посадкой на Землю. Поэтому заключение брата-астронавта неверно. СТО предсказывает, что при возвращении на Землю он действительно окажется моложе своего брата, оставшегося на Земле.

Эффекты замедления времени пренебрежимо малы, если скорость космического корабля гораздо меньше скорости света c. Тем не менее, удалось получить прямое подтверждение этого эффекта в экспериментах с макроскопическими часами. Наиболее точные часы – это атомные часы на пучке атомов цезия. Эти часы «тикают» 9192631770 раз в секунду. Американские физики в 1971 году провели сравнение двух таких часов, причем одни из них находились в полете вокруг Земли на обычных реактивных лайнерах, а другие оставались на Земле в военно-морской обсерватории США. В соответствии с предсказаниями СТО, путешествующие на лайнерах часы должны были отстать от находящихся на Земле часов на (184 ± 23)·10–9 с. Наблюдаемое отставание составило (203 ± 10)·10–9 с, то есть в пределах ошибок измерений. Через несколько лет эксперимент был повторен и дал результат, согласующийся со СТО с точностью 1 %.

В настоящее время уже необходимо принимать во внимание релятивистский эффект замедления хода часов при транспортировке атомных часов на большие расстояния.

СТО устанавливает зависимость пространства и времени от скорости движения материальных тел. Кроме того, она устанавливает неразрывную связь пространства и времени, поскольку они изменяются синхронно, и притом в противоположных направлениях: при больших скоростях движения тел их линейный размер сокращается в направлении движения, а ритмика течения времени растягивается. Поэтому рассмотрение физических событий должно относиться е единому четырехмерному пространственно-временному континууму.

Закон пропорциональности массы и энергии является одним из самых важных выводов СТО. Масса и энергия являются различными свойствами материи. Масса тела характеризует его инертность, а также способность тела вступать в гравитационное взаимодействие с другими телами. Важнейшим свойством энергии является ее способность превращаться из одной формы в другую в эквивалентных количествах при различных физических процессах – в этом заключается содержание закона сохранения энергии. Пропорциональность массы и энергии является выражением внутренней сущности материи. Формула Эйнштейна

E0 = mc2

выражает фундаментальный закон природы, который принято называть законом взаимосвязи массы и энергии. 

Следует обратить внимание, что при малых скоростях движения (υ << c) формулы СТО переходят в классические соотношения: l ≈ l0 и τ ≈ τ0. Таким образом, классические представления, лежащие в основе механики Ньютона и сформировавшиеся на основе многовекового опыта наблюдения над медленными движениями, в специальной теории относительности соответствуют предельному переходу при β = υ / c → 0. В этом проявляется принцип соответствия.