Платон и математика

Математика играет исключительную роль в системе Платона, уступая лишь диалектике. “Не геометр не войдет” – написано над воротами Академии, Те, кто не были сведущи в музыке, геометрии и астрономии вообще не принимались в платоновскую Академию. Ксенократ, второй после Платона глава Академии (сколарх), сказал человеку, не знакомому ни с одной из этих наук: “Иди, у тебя нечем ухватиться за философию”. Неудивительно, поэтому, что среди учеников Платона были крупные математики, такие как Архит, Теэтет, Евдокс. Альбин, написавший учебник платоновской философии, сообщает: “Математику Платон допускает ради того, что она, по его мнению, изощряет мысль, оттачивает душу и позволяет достичь точности в исследовании бытия. Арифметика отучает нас от приблизительности, неопределенности и недостоверности чувственно воспринимаемого, помогает познать сущность. Так же и геометрия весьма способствует познанию блага, если, конечно, подходить к ней не ради практических целей. Крайне полезна и стереометрия. Полезна и астрономия, четвертая дисциплина, рассматривающая движение звезд по небу и самого неба, создателя ночи и дня, месяцев и лет. Пятой математической наукой является музыка”. Такова иерархия математических наук (по степени приближенности к благу).

Изучение этих дисциплин есть своего рода введение к рассмотрению сущего: в своем стремлении постичь сущее геометрия, арифметика и связанные с ними дисциплины грезят о нем, хотя и не способны увидеть его въяве. Платон сам математиком не являлся, но вокруг его группировались выдающиеся математики того времени. Евдокс, непосредственный ученик Платона, сам учитель Евклида. Архит – пифагореец, но очень близкий платоновской Академии. Явно платоновские идеи проскальзывают в мировоззрении Архимеда (стеснялся своих технических достижений). Авторитет и влияние Платона на греческих математиков было весьма велико. Как водится, в истории сохранился яркий отрицательный пример такового. Плутарх пишет: “Знаменитому и многими любимому искусству построения механических орудий положили начало Евдокс и Архит, стремившиеся сделать геометрию более красивой и привлекательной, а также с помощью чувственных, осязаемых примеров разрешить те вопросы, доказательство которых посредством одних лишь рассуждений и чертежей затруднительно. Но так как Платон негодовал, упрекая их в том, что они губят достоинство геометрии, которая от бестелесного и умопостигаемого опускается до чувственного и вновь сопрягается с телами, требующими для своего изготовления длительного и тяжелого труда ремесленника, механика полностью отделилась от геометрии и, сделавшись одной из военных наук, долгое время вовсе не привлекала внимания философов”. Тем не менее, само отношение и высокий ранг математики в системе наук Платона, а также гипотетико-дедуктивный метод – дитя Платона, который находит в математике свой апофеоз в “Началах…” Евклида, делают вклад Платона в математику огромным.

Вторая школа (после софистов), от которой отталкивался Платон при построении своей философии это натурфилософия. В диалоге “Федон”, устами Сократа дается следующая характеристика натурфилософского знания:
“В молодые годы, - говорит Сократ, - у меня была настоящая страсть к тому виду мудрости, который называют познанием природы. Мне представлялось удивительным и необыкновенным знать причину каждого явления: почему что рождается и почему погибает и почему существует. И я часто метался из крайности в крайность, и вот какие вопросы задавал себе в первую очередь: когда теплое и холодное, взаимодействуя, вызывает гниение, не тогда ли, как судили некоторые, образуются живые существа? Чем мы мыслим – кровью, воздухом или огнем? Размышлял я и о разрушении всего существующего и о переменах, которые происходят в небе и на земле, - и все для того, чтобы, в конце концов, счесть себя совершенно непригодным к такому исследованию...” ибо “…утратил понимание даже того, что до этого казалось понятным, …окончательно ослеп и разучился даже тому, что знал прежде”.

Отсюда ясно, что Платон иронизирует по поводу понятий, которыми оперировала старая натурфилософия, которые носили метафорический характер. Что значит “мыслить кровью, воздухом или огнем”? Разумеется, говоря о том, что мы мыслим, допустим, огнем, натурфилософ хотел тем самым показать, что из всех природных стихий огонь – самая легкая, быстрая, подвижная, и в этом его сходство с мышлением. Но ведь это метафора, т.е. аналогия, а не логическое понятие. А всякая метафора фиксирует только одну сторону явления, и, следовательно, явление можно описать бесчисленным множеством метафор, отражающим бесчисленное множество связей и сторон явления.

Платон устами Сократа указывает на отсутствие доказательства положения, которое выдвигает натурфилософ, ибо с помощью метафоры можно только показать, но не доказать явление. Он (натурфилософ) может указать аналогию в виде определенного частного явления, которая им распространяется на весь мир вообще. Метафорическое мышление родственно мифологическому, которое также не требует доказательства. Любое явление можно объяснить через что-то другое, а этих других – много. У Платона есть пример. Так двойку можно определить и как результат деления на две части одной какой-то единицы и как результат сложения двух раздельно существовавших единиц. Но ведь тогда мы даем разные определения двойки, мы берем ее в разных отношениях, значит, и двойки наши будут разные. То, что эти разные двойки подтверждают современные взгляды на природу числа (Р. Штейнер, Г. Кантор, Э. Биндель), которые наглядно демонстрируют противоположность 2-х подходов к числу:

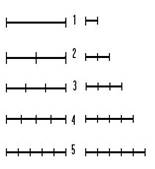
связывая правый столбец с механистической (аналитической) философией и наукой, а левый с органической (синтетической).

Поэтому по Платону, прежде чем что-либо определять, надо понять, что такое определение. Прежде, чем что-либо понимать, надо выяснить, что такое понятие, прежде, чем мыслить надо дать себе отчет, что такое мышление. Натурфилософы оперировали в своих построениях такими понятиями как “влажное и сухое”, “холодное и теплое”, “сладкое и горькое”, “твердое и мягкое”. Исходя из этих противоположностей, они давали определение и объяснение природных явлений и процессов. Но эти определения, согласно Платону, не могут дать никакого доказательного знания, ибо они в строгом смысле определениями не являются. Натурфилософы имели, в сущности, дело с неопределенно-количественными характеристиками, с теми самыми “более или менее”, которые не могут ухватить определяемый предмет, не могут ввести его в твердые границы, ибо не располагают для этого мерным отношением – числом.

2. Платоновская математическая программа и ее выходы в физику. “Молекулярное” учение Платона. Свое представление о природе Платон выразил в диалоге “Тимей”. Платон считал, что чувственный мир (природа) не может быть предметом научного знания не только высшего (диалектика), но и промежуточного, математического уровня. Физика, по Платону, не может и не должна претендовать на статус науки – таковой является лишь математика “…нам приходится довольствоваться в таких вопросах правдоподобным мифом, не требуя большего”. О вещах, относящихся к миру чистых идей, можно судить, согласно Платону, с уверенностью, все взвешивая, испытывая и разбирая чисто диалектическим путем. В области же природы, где наши знания основываются, главным образом, на наблюдениях, мы можем иметь суждение лишь “о наиболее правдоподобном”. Причем и при рассмотрении природы “наиболее важными ему кажутся прежде всего математические законы природы, находящиеся за явлениями, а не сам многогранный мир явлений. Никакая другая задача науки о природе не кажется ему столь существенной, как задача открытия неизменных законов в постоянно меняющихся явлениях”.

И, тем не менее, по мнению некоторых современных исследователей “всего лишь правдоподобная” модель физического мира Платона – является наиболее детально разработанным атомно-молекулярным учением античности. Впрочем, многие историки физики с этим не согласны. Некоторые историки с этим не согласны и считают деятельность Платона реакционной и не представляющей интереса.

Предмет физики по Платону – изучение природы универсума (термин, обозначающий всю объективную реальность во времени и пространстве, у Платона – видимый мир), человек как живое существо и его место в мире, промысел божий о мировом целом и подчинение ему других богов, отношения между людьми и богами.

Универсум имеет 3 начала.

1. Материя. Платон называет ее “принимающей любые оттиски”, всеприемницей, кормилицей, матерью и пространством. Ей свойственно вмещать всякое рождение, причем сама она остается лишенной формы, качества и вида, хотя и создает в себе их слепки и отпечатки. Материя, чтобы полностью вместить все виды, должна быть субстратом, совершенно их лишенным, не имеющем – ради восприятия видов – ни качества, ни вида.

2. Помимо материи Платон в качестве начал признает образец – идеи. Для материи идея есть мера. У Космоса, в частности, тоже есть свой первообраз.

3. Бог-демиург (создатель).

Демиург создает из той сущности, которая неделима и вечно тождественна (образец-идея) и той, которая претерпевает разделение в телах (материя) путем смешения в третий, средний вид сущности – душу. Затем все три начала слил в единую идею живого Космоса, силой принудив не поддающуюся смешению природу к сопряжению с тождественным. Космос у Платона – живое и одушевленное тело, образцом и подобием этого живого и одушевленного космоса является и человек.

Однако, на этом не завершается создание космоса. Полученное единое целое Демиург, в свою очередь, разделил на нужное число частей (в соответствии с пифагорейским учением о пропорциональных отношениях) как 1/2/3/4/8/9/27. В этих отношениях выражается отношение сфер, вращающихся вокруг Земли, расположенной в центре, Луны (1), Солнца (2), Венеры (3), Меркурия (4), Марса (8), Юпитера (9), Сатурна (27). Последняя сфера – сфера неподвижных звезд, которая занимает особое место среди остальных сфер. В этих “долях” выражаются все виды пропорциональных отношений между числами: геометрическая, арифметическая и гармоническая пропорции. Далее идет достаточно сложная мистико-числовая теория.

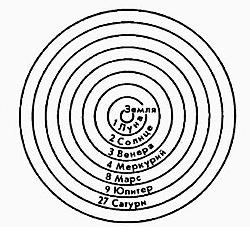
Как видим, космогония Платона сама в значительной мере мифологична. Перейдем к другому уровню устроения материи.

Что есть природные стихии, элементы, из которых состоят вещи? Платон, как и Эмпедокл, выделяет четыре природных элемента: земля, вода, воздух, огонь. Демиург, по Платону, приступая к построению Космоса, начал с того, что упорядочил эти четыре рода с помощью образов и чисел. Платон говорит о частицах 4-х видов, соответствующих 4-м первообразам, первоэлементам, но в отличие от Эмпедокла, Демокрита и Эпикура, он подчеркивает их способность превращаться друг в друга. Скорее это четыре структурных, агрегатных состояния, ибо Платон подчеркивает: «имеющие свойства земли или воды, или воздуха, или огня». К землеобразным телам Платон относит камни, руды и тому подобные практически неплавящиеся вещества. Все расплавляющиеся тела относятся к “водообразным”, все паро- и газообразные – к воздухообразным, а все воспламеняющиеся пары – к огнеобразным.

Но сущность первооснов определяется не тем, что мы различаем как свойства природных элементов и вообще воспринимаем с помощью нашего тела – что, например, огонь красен и горюч, а земля плотна, тяжела и непрозрачна и т.д. - все эти свойства чаще ничего не говорят нам о том, что такое огонь и земля сами по себе. Чтобы узнать это, нужно выяснить, с помощью каких образов и чисел упорядочил бог эти стихии, т.е. нужно выяснить математические определения этих стихий. И Платон получает геометрические образы первоэлементов исходя их следующих соображений:

- Огонь, земля, вода и воздух суть тела, следовательно, должны быть объемны. Четыре геометрических образа должны все же обуславливать основные физические свойства (твердость, плавкость, воздухообразность, огнеобразность)

- Первостихии по крайне мере 3-х видов (вода, воздух, огонь) должны превращаться друг в друга.

- “Научная эстетика”. Первообразы (идеи) стихий должны быть правильными, эстетически и математически совершенными, а не как у Демокрита атомы – по форме крючки, веретена и т.п.

Как раз при жизни Платона математик Теэтет разработал геометрию правильных многогранников. Платон воспользовался этой математической новинкой.

Как известно из геометрии, возможны пять видов правильных многогранников – тетраэдр(1), октаэдр(2), икосаэдр(3), куб(4) и додекаэдр(5). У первых трех многогранников все грани одинаковы и представляют собой равносторонние треугольники, куб имеет квадратные грани, а додекаэдр – пятиугольные. Платон приписал куб первообразу земли, потому что куб – самое устойчивое из геометрических тел, а земля отличается именно своей неподвижностью, устойчивостью. Огню – тетраэдр, ибо последний наиболее, вроде бы, сходствует с подвижной и легкой стихией огня, и к тому же имеет наиболее острые грани и углы (режет, жжет, всюду легко проникает). Аналогичны рассуждения о воздухе – октаэдре и воде – икосаэдре.

“Земле мы придаем кубическую форму – ибо среди этих четырех видов земля является наименее подвижной, а среди тел – наиболее крепкой. Равносторонняя четырехугольная плоскость и по своим частям и как целое неизбежно устойчивее, нежели равносторонняя треугольная. Приписывая земле эту основу, мы получаем наиболее вероятное представление. Воде мы, напротив, припишем из прочих возможностей менее трудноподвижную фигуру, огню наиболее легкоподвижную форму, а воздуху – промежуточную. Наименьшую телесность мы придаем огню, наибольшую, напротив, - воде, а воздуху – промежуточную. Из всех их то, что имеет меньше всего граней, должно быть наиболее подвижным и проникающим, поскольку оно наиболее остроконечно из всех прочих и к тому же легче из всех, ибо оно состоит из наименьшего числа однородных частей. Второе должно обладать этим во второй степени, а третье – в третьей”.

Как уже говорилось, пифагорейцы и Платон считали элементом n-мерной фигуры n-1 – мерную фигуру. Следовательно, геометрические образы, т.е. объемные фигуры состоят из плоскостей, притом всякая плоскость состоит из треугольников, причем “первичны два прекраснейших треугольника – прямоугольные: неравнобедренный и равнобедренный. Один угол неравнобедренного треугольника прямой, другой две трети прямого, третий – одна треть

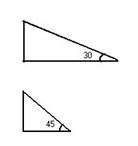
Из этих-то треугольников и состоят грани многогранников. На каждой из треугольных сторон тетраэдра, октаэдра и икосаэдра укладывается 6 неравносторонних треугольников, на каждой грани куба – 8 равнобедренных.

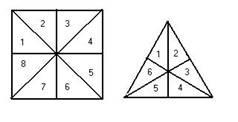
Эти то треугольники и являются “атомами” Платона (он, впрочем, не употреблял такого термина). Куб состоит из 8*6=24 равнобедренных прямоугольных треугольников, тетраэдр из 6*4=24 неравнобедренных, октаэдр - 6*8=48, икосаэдр – 6*20=120 прямоугольных треугольников. Последние три пустотелые фигуры могут, распадаясь на составляющие их треугольники, складываться заново, превращаясь друг в друга. Только куб (и додекаэдр), распадаясь, не могут превращаться затем в другую фигуру. Фигуры элементов настолько малы, что “каждое отдельное составляющее всех этих видов само по себе не может быть видимо нами, но множество их становится заметным”.

Многогранники вовсе не эквивалентны атомам, как это иногда указывается, а скорее соответствуют чему-то вроде “молекул” (а может быть и кристаллов), т.е. структурных составляющих данного агрегатного состояния. “Этим четырем – не буквам, клянусь Зевсом, а слогам, - космический демиург придал очертания пирамиды, куба, октаэдра, икосаэдра. А вот треугольники – своеобразные “атомы”, хотя о делимости или неделимости их Платон нигде не говорит, судя по всему, считая подобные термины неприемлемыми.

Существуют разногласия во мнениях, считать ли эти треугольники физическими частицами (имеющими, пусть и малый, объем и массу) или чисто математическими конструкциями. Действительно, Платон упоминает о весе многогранников, он упоминает, что треугольники в реальных многогранниках скреплены между собой бесчисленным множеством штифтов, незримых, благодаря их малости, между тем, как в идеальной модели (идее) они скреплены нерушимыми связями. Большинство же имеет второе суждение. Еще Аристотель отмечает: “Платон в Тимее говорит, что материя и пространство – одно и то же”. А намеки Платона на “физичность” можно отнести за счет того – “не истинного, а лишь правдоподобного” – способа рассуждения, о котором упомянуто ранее. Судя по всему, Платон действительно не разделял материю и пространство. Материя (атомы) понимается не как вещество, а как пространство. Треугольники представляются как дискретные порции континуума. В. Гейзенберг отмечает близость фигур и треугольников как математических элементов идеям современной физики о том, что элементарная частица есть математическая формула, только значительно более сложная, чем “геометрическая формула” Платона.

Итак, вода, воздух и огонь могут переходить друг в друга. Землееобразные же тела не могут участвовать в подобных превращениях. В тех случаях, когда “землеобразные тела” как будто плавятся, Платон рассматривает такой переход лишь как временное расчленение кубических частиц под ударами проникающих в промежутки между ними “острых и колючих” тетраэдров огня. Также и растворение твердых веществ в воде происходит при благоприятных обстоятельствах, когда октаэдры жидкого растворителя проникают в промежутки между кубами твердого тела и, так сказать, размывают его. Процессы взаимного превращения многогранников осуществляются благодаря непосредственным столкновениям движущихся структурных частиц с частицами огня или друг другом. Движения же частиц возникают исключительно вследствие наличия неоднородностей. Платон подчеркивает, что в строго однородной среде никогда не может возникнуть движение.

Все эти превращения он представляет себе настолько наглядно, что даже составляет уравнение, которое в современном написании имеет вид:

1 “вода” = 2 “воздуха” + 1 “огонь”

Или, по числу первичных треугольников 120 = 2*48+24. Это первое в истории науки уравнение баланса. Более того, оно мало отличается от современного термохимического уравнения: H2O=H2+0.5O2+Q, Где слева находится одна вода, а справа 1,5 газа («воздуха») и Q - тепловой эффект реакции (“огонь”). Тем более, что в “огне” Платон различал несколько видов: свет, пламя, а также то, что остается от огня в накаленных телах, когда пламя потушено, т.е. некая материя тепла (теплород – понятие очень важное в истории химии).

Далее, Платон вовсе не уподобляет все водообразное именно воде. Существует множество водообразных икосаэдров, отличающихся только размерами, каждый из которых соответствует конкретному водообразному веществу. Также и для остальных агрегатных состояний. Земля же это не столько твердое, сколько неплавящееся вещество. “Что касается тел, которые мы назвали плавкими, то наиболее плотное среди них, образуется из наиболее тонких и наиболее однородных частиц … и характеризуется своим блеском и желтым цветом. Это золото. Нечто близкое золоту по составным частям (“молекулам”), но заключающее в себе более одного их вида (по размерам), а по плотности стоящее еще выше золота, принявшее в себя для увеличения твердости малую и тонкую часть земли, но вследствие больших внутренних промежутков более легкое, образовало один из блестящих и застывших видов воды – бронзу. Но то, что ей примешано от земли, получило название ржавчины, когда от давности оба рода отделяются друг от друга, и примесь вновь обособляется. Вовсе не трудно дать себе отчет в других явлениях такого рода, если следовать выявлению наиболее вероятного”.

Вот, например, процесс затвердевания жидкости (это не процесс перехода икосаэдра в куб, а процесс уплотнения икосаэдров). “Бывает, что огонь вновь удаляется из воды (между икосаэдрами тетраэдры), а поскольку он уходит не в пустоту, то окружающий воздух, теснимый огнем, давит на еще легкоподвижную, жидкую массу, заставляет ее заполнить те промежутки, где ранее находился огонь, и вплотную прижимается к ней. Сжатая таким образом жидкость, вновь становится однородной, поскольку огонь, создавший в ней неоднородность, удалился, и она снова превращается в сплошную массу. Удаление огня было названо охлаждением, а уплотнение, сопровождающее этот уход огня, получило название затвердевания”. Т.о. “жидкость” жидка, когда в ней присутствуют неоднородности (связанные с наличием огня) и, тем самым, ее частицы приобретают возможность движения. Существуют также виды жидкости, которые в силу наличия частиц (икосаэдров) разных размеров неоднородны, а, следовательно, подвижны и жидки.

Надо сказать, что эти рассуждения значительно более ясны, правдоподобны и близки современным представлениям, чем рассуждения об этих же явлениях Эпикура, да и всех других философов античности. Человеку, знающему учение о фазовых равновесиях, подход Платона представляется весьма плодотворным. Дорфман на основе текста “Тимея” формулирует три правила фазового равновесия:

1. Однофазная, однородная система находится в устойчивом равновесии, и в ней не происходят никакие движения или изменения.

2. В двухфазной системе фаза, количественно преобладающая и более устойчивая, постепенно либо уничтожает, либо вытесняет менее устойчивую фазу.

3. Наоборот, в двухфазной системе менее устойчивая фаза или находящаяся в меньшем количестве, должна либо исчезнуть путем превращения в преобладающую фазу, либо выделиться из смеси.

Таким образом, за счет проясненности понятий и самой логики рассуждений и убежденности (родственной пифагорейской), что строение и функционирование Вселенной основано на неизменных количественных закономерностях “идеалист” Платон способен объяснить природные явления более точно, чем современные ему “материалисты” (Демокрит, Эпикур). Учение Платона о первообразах имело развитие. Прокл (410- 485 гг. н.э.) подчеркивал, что “концепция о способности острого угла вызывать нагревание, ошибочна. Помимо этого (для режущей способности) требуется еще быстрота движения”. Так впервые была высказана идея о том, что частички огня или тепла должны обладать быстрым движением.

Плодотворность школы Платона объясняется ее не догматичностью в физике. Прокл: “…возможно, что пифагорейцы и Платон вовсе не постулировали строение предметов из треугольников как нечто абсолютное. Эта их процедура подобна тому, как различные астрономы строили гипотезы, основанные на твердом убеждении, что особенности небес не являются тем, чем они кажутся, но можно "спасти явление" (рационально объяснить), если принять за основу предположение о равномерном и круговом движении небесных тел. Подобно этому пифагорейцы, принципиально предпочитая количественное качественному, приняли за элементы тел эти геометрические формы как наиболее отвечающие определенному принципу, как наиболее совершенные с точки зрения подобия и симметрии и, притом, казавшиеся им достаточными для интерпретации физических явлений”. В этой фразе даны основные принципы научного, физического моделирования.

В целом, главной заслугой Платона для физики является то, что своей “молекулярной теорией” он впервые в истории строит вариант математической физики, не реализованный никем потом вплоть до нового времени. В физике он остается верным своей математической программе, считая, что в мире природы достоверное знание мы можем получить ровно в той мере, в какой раскроем математические структуры этого природного мира.