Математика в системе научных знаний

То, что представленная на рис.1.1. схема далеко не отражает всей сложности современного научного знания, можно показать также и на примере математики. Математика среди всех наук занимает исключительное положение. Это становится очевидным, если попытаться найти  для неё определённое место в нашей схеме научного знания. Такая попытка сразу покажет, что точное место найти не возможно, поскольку математика – это нечто особенное, что имеет отношение ко всем наукам, хотя и в разной степени.

Возникновение математики является примером чёткого и крайне полезного применения принципа иерархии. Очень важным в жизни древних людей было появление способности  передавать друг другу сведения о количественных характеристиках природных явлений. Для успешного выживания нужно было знать, сколько полезных растений или животных обитало поблизости на той или иной территории. Необходимо было уметь сопоставлять численность воинов соседних племён с численностью собственных воинов и т.д. Всё это и многое другое заставило человека научиться считать, в связи с чем должно было появится понятие количества. Весьма вероятно, что поначалу количественные сведения передавались людьми друг другу с помощью жестов, пальцами руки. Первые попытки записи количества известны в археологии в виде насечек, нанесённых на какой-либо материал (дерево, камень, глина). Каждый набор насечек соответствовал определённому количеству каких-либо предметов. При такой записи каждое добавление следующей насечки требует нового названия данному количеству. Этот подход не вызывает никаких затруднений, пока число не превышает одного – двух десятков. Но продвижение в область больших количеств показывает бесперспективность такого подхода, поскольку приводит к необходимости придумывать и запоминать бесконечно большое количество названий. Эта трудность была преодолена благодаря использованию принципа иерархии. Развитие мышления позволило сделать вывод, что достаточно использовать всего десять названий (десять знаков, включая нуль) для обозначения любых количеств. То есть после одного десятка нужно начинать считать десятками, затем десятками десятков (сотнями), десятками сотен (тысячами) и т.д.:

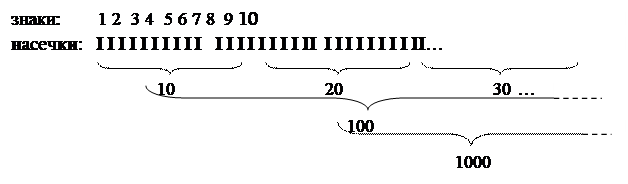
Дальнейшее развитее математики показало, что подобная иерархическая система записи чисел может быть основана не только на числе десять, но и на любых других числах не меньше двойки. Практическое применение в современной математике получили двоичная, восьмеричная и шестнадцатеричная системы исчисления. В частности, при современном способе записи горизонтальной строкой в двоичной системе на первом месте справа налево указывается количество единиц, на втором - количество двоек, на третьем – количество двоек двоек (четвёрок), на четвёртом – восьмёрок и т.д.

Начавшись с натурального элементарного счёта, математика развилась до современной очень обширной области знаний. Особое положение математики определяется тем, что если каждая из остальных наук занимается получением знаний о какой-то отдельной области действительности и устанавливает специфические законы в этой области, то математика является языком, на котором эти законы формулируются. Первым, кто дал такое определение математики, был Галилей. Ему же принадлежит и первенство в применении строгих математических методов при изучении природных явлений.

Любой язык можно определить как систему знаков и правил оперирования с этими знаками. Эта система используется для описания явлений и процессов, происходящих в окружающем мире. Описание мы производим и с помощью обычных языков. В таком случае нужно определить, в чём принципиальное отличие математики? Математика – это специально разработанный язык. Значение каждого символа и правила в математике строго оговаривается и является общепринятым для всех людей.

Обычные (естественные) языки, в отличие от математики, возникают стихийно,  самостоятельно у каждой нации, они более громоздки и неоднозначны. В таких языках одним словом могут называться разные явления и, наоборот, одно и то же явление может обозначаться разными словами.

Строгость и однозначность математики определяется тем, что каждый вводимый символ (или понятие) отражает определённую, существенную особенность окружающих явлений, отвлекаясь от всех сторон, свойств, которые можно считать несущественными. Такой подход называется абстрагированием. В качестве примеров абстрактных понятий можно назвать понятия «точка», «линия», «поверхность», «число» и т.д.

Математикой мы овладеваем с помощью обычного языка. Поэтому всё, что записано математически, можно сформулировать и записать на обычном языке, но это будет громоздко и неудобно. Преимущество математической записи в том, что она является очень краткой, сжатой, удобной в применении. А математические высказывания выглядят очень строгими, точными и убедительными. Вот несколько примеров.

Если имеется функция y = f(x), то её производная обычным языком определяется как «предел, к которому стремится отношение приращения функции к приращению аргумента при приращении аргумента, стремящимся к нулю». В математическом виде всей этой фразе соответствует запись: yI.

Одно из направлений развития математики - это поиск более совершенных и лаконичных форм записи. Это можно продемонстрировать ещё одним примером. Математическая запись 10100 без использования операции возведения в степень представляет собой единицу, после которой записаны сто нулей:

10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000.

Такая запись явно неудобна. Записав число, Вы сразу же начнёте сомневаться: а нет ли ошибки в количестве нулей? Это потребует повторного пересчёта. И если пересчёт покажет иное количества нулей, придётся пересчитать в третий раз. Теперь, если совпадут по количеству два из трёх пересчётов, можно предположить, что совпадающие варианты являются правильными. Но и после этого сомнение останется, поскольку существует вероятность повторения ошибки. Придётся сосчитать ещё один раз, и в случае третьего совпадения результатов  можно быть почти(?!) уверенным в правильности записи.  Однако и такая ситуация может не убедить скептиков в существенных преимуществах математики. Тогда надо напомнить, что здесь оба варианта представляют собой математические записи, поэтому преимущество более совершенного варианта не выглядит радикальным (очень существенным).

Теперь попробуем представить себе, как могла бы выглядеть запись данного числа при отсутствии десятичной системы исчисления, т.е. попытаемся изобразить её в виде насечек. Предварительно отметим, что, например, число атомов во Вселенной оценивается в современной науке величиной приблизительно 1070 ÷ 1080. Это означает, что без математики для записи числа порядка 10100 нужно иметь в своём распоряжении много миллиардов вселенных и умудриться во всех этих вселенных на каждом атоме поставить засечку!!! После такого примера вряд ли можно сомневаться в преимуществах математики.

Наиболее математизированными разделами естествознания являются физика и астрономия. Это объясняется относительной простотой изучаемых ими явлений, в которых число взаимодействующих факторов относительно невелико. Вообще-то факторов много, но большинством из них, как правило, можно пренебречь. В качестве ярких примеров открытий, сделанных в этих науках с помощью математики, можно привести открытие последней из известных планет солнечной системы - Плутона и предсказание существования некоторых элементарных частиц за несколько лет до их экспериментального обнаружения.

В первом случае сравнение фактически наблюдаемых параметров движения дальних планет с параметрами, рассчитанными на основании законов механики, показало их некоторое несоответствие. Но это несоответствие исчезало, если в расчёты вводились определённые параметры ещё одной, пока не наблюдаемой планеты. Наведение телескопов в заданную расчётную точку и в заданное время показало, что, действительно, такая планета существует.

Аналогично в середине ХХ столетия были экспериментально обнаружены и элементарные частицы - только через несколько лет после их «математического предсказания» на основании разработанной ранее теории.

Эти и подобные им достижения в сочетании со строгостью, точностью и убедительностью математических доказательств могут создать впечатление, что математика - это инструмент для получения новых глубинных знаний об окружающем мире. Такой вывод ошибочен, поскольку любой язык, в том числе и математический, – это только средство общения и описания действительности, что, несомненно, является частью познавательного процесса, но никак не источником нового знания.

К сожалению, современные люди, имея в своём распоряжении язык и хорошо научившиеся говорить, настолько уверовали в силу слова, что во множестве случаев своё незнание восполняют пустой болтовнёй, набором слов, абсолютно не соответствующим никаким объективным явлениям природы. Так, появляются выдуманные «одарёнными» умами понятия: «душа», «дух», «аура», всякие «чакры – шмакры» и прочая дребедень. Если за подобными понятиями и стоят какие-либо объективные явления, то они должны быть изучены научными методами, получить соответствующее научное объяснение.

Точно так же за многими страницами математических символов и многоэтажных формул, которые магически завораживают и сбивают с толку, может ничего не стоять в действительности, кроме стремления их авторов поупражняться в математических изысках.

Новые знания получаются не разговорами, рассуждениями или расчётами, а практическим опытом, при взаимодействии с окружающей природой с помощью органов чувств. Язык, в том числе и математический, служит лишь для удобного накопления, обобщения, анализа знаний и передачи знаний от одного человека к другому.

Математика представляет собой абсолютно бесполезный набор закорючек, если использующий её человек не имеет практического опыта и не может определить соответствие между математическими символами и явлениями действительности. Покажем это на очень простом примере. Запишем две формулы:

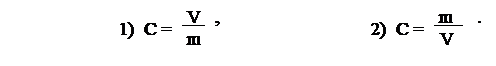
Почти любой школьник 6-7 класса сможет объяснить математическое значение каждого символа в этих формулах. А именно, что символы   С, V  и m обозначают некоторые числа. Горизонтальная черта означает, что верхнее число следует разделить на количество частей, равное нижнему числу. А знак  =  означает, что число С равно тому, что получится в результате деления. Но подавляющее количество даже вузовских студентов (чаще гуманитарных специальностей) оказываются в полном замешательстве, когда им сообщают, что одна из этих формул определяет такое явление природы, как концентрация вещества, и нужно указать, какая из этих формул верна? Специальные многократные опросы показали, что правильные ответы составляют не более 10%. Это объясняется тем, что у отвечающих при достаточном уровне математических знаний нет практического опыта в данной области. В то же время студенты биолого-химического факультета, которые на практических занятиях регулярно готовят различные растворы, дают правильный ответ не менее чем в 90% случаев. Но эти же студенты не могут определить, какая из двух следующих формул соответствует закону Ома:  

несмотря на то, что большинство правильно называют R сопротивлением,U напряжением, а I силой электрического тока.

Отсюда следует весьма важный вывод: математика может успешно применяться только при глубоком знании природных процессов и явлений, когда исследователь, хорошо зная математические символы и математические законы, может правильно соотносить их с определёнными свойствами реальной действительности.

Для некоторых читателей на всякий случай укажем, что правильными из рассмотренных являются формулы 2) и 3).

То, что математика тесно связана с практическим опытом можно, показать и на хорошо известных исторических примерах возникновения математических идей с последующим их развитием в новые разделы математики.

Так, теория вероятностей появилась как инструмент предсказания выигрыша в карточных играх. И, несмотря на то что первоначально эта теория использовалась для удовлетворения, можно сказать, низменных потребностей азартных игроков, в дальнейшем она явилась мощным толчком в развитии многих отраслей науки и техники, о чём можно судить хотя бы по масштабам современного применения математической статистики.

Другим примером является возникновение дифференциального и интегрального исчисления, когда с развитием физики понадобилось рассчитывать реальные перемещения тел, движущихся с переменными скоростями и вычислять площади фигур сложной формы. В современной науке это направление, получившее название математического анализа, стало одним и наиболее мощных инструментов описания громадного множества природных явлений, параметры которых представляют собой переменные величины.

И, наконец, абсолютно бесспорным аргументом в пользу громадной роли математики в современном мире является её вклад вместе с физикой и химией в развитие компьютерной техники. Компьютеры на много порядков повышают производительность труда и расширяют наши возможности в самых различных отраслях деятельности: науке, промышленности, сельском хозяйстве, медицине, образовании, военном деле. Правда, для последней из указанных сфер выражение «производительность труда» может иметь некоторый аморальный оттенок.