В ньютоновской механике при переходе от одной инерциальной системы к другой, движущиеся с постоянной скоростью относительно первой применяются преобразования Галлия, которые основаны на двух аксиомах. Первая: время течет одинаково во всех инерциальных системах отсчета. Вторая: расстояние или размеры тела остаются неизменными в различных инерциальных системах.
Подвижная система координат движется со скоростью 
=const. Сходственные оси обеих систем координат попарно параллельны. 
радиус вектор, определяющие положение тела в подвижной системе координат. 
-радиус-вектор, определяет положение тела в неподвижной системе координат. Тогда 
.
Проекция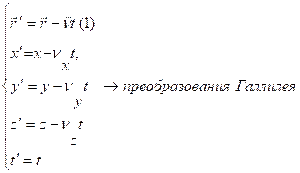 
Обычно оси координат проводят так, чтобы система 
двигалась вдоль положительного направления оси Х.
Тогда преобразования Галилея: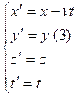 
Поделим обе части уравнения(1) на t, тогда получим 
(2), где 
- скорость тела в подвижной системе координат, 
- скорость тела в неподвижной системе координат, 
- скорость движения подвижной системы координат относительно неподвижной. Ускорение и в подвижной и неподвижной системе одинаковы: 
. Силы, действующие в обеих системах одинаковы: 
, зависят только от взаимного расположения тел и от относительных скоростей ( друг относительно друга). Формула (2) справедлива для всех случаях жизни за исключением скорости света. Согласно выражению (2) для скорости света мы должны написать: 
, знак (+), если приемник световых волн движется навстречу, а знак (-), когда приемник удаляется от источника света. Однако бесчисленные эксперименты (опыты Моля, эксперименты с лазером) показали, что 
.
Поможем написать любую работу на аналогичную тему