Уравнения Эйлера

          Выделим в жидкости конечный объём. Полная сила, действующая на выделенный объём жидкости, равна интегралу

.

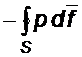          взятому по поверхности рассматриваемого объёма. Преобразуем его в интеграл по объёму, имеем

.

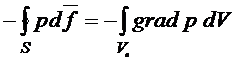          Отсюда видно, что на каждый элемент объёма  жидкости действует со стороны окружающей его жидкости сила - .

Тогда на единицу объёма жидкости действует сила.

          Мы можем теперь написать уравнение движения элемента объёма жидкости, приравняв силу  произведению массы  единицы объёма жидкости на её ускорение

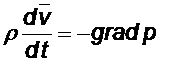.                                                 (1)

          Стоящая здесь производная  определяет не изменение скорости жидкости в данной неподвижной точке пространства, а изменение скорости определённой передвигающейся в пространстве частицы жидкости. Эту величину необходимо выразить через величины, относящиеся к неподвижным в пространстве точкам.

          Изменение скорости данной жидкой частицы в течение времени  складывается из двух частей:

          - из изменения скорости в данной точке пространства  в течение времени ;

- из  разности  скоростей  (в один  и тот  же момент времени)  в двух точках, разделённых расстоянием , пройденным рассматриваемой частицей в течение времени.

          Первая из этих частей равна

,

где производная берётся  при постоянных   x,y,z, т.е. в заданной точке пространства.

          Вторая часть изменения скорости равна

 .

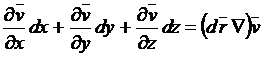          Таким образом,

  ,

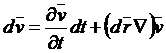          или, разделив обе скорости равенства на  dt

 .

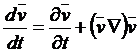          Подставив полученное соотношение в (1), получим

.

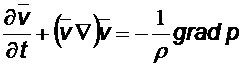          Полученное уравнение движения жидкости - уравнение Эйлера (1755), и является одним из основных в гидродинамике.

          Если жидкость находится в поле тяжести, то на каждую единицу её объёма действует ещё сила , где есть ускорение силы тяжести. Эта сила должна быть прибавлена к правой стороне уравнения, и уравнение принимает вид:

.

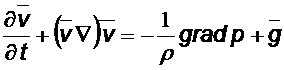          При выводе уравнений движения мы совершенно не учитывали процессов диссоциации энергии, которые могут иметь место в текущей жидкости вследствие внутреннего трения (вязкости) в жидкости и теплообмена между различными её участками.

          Отсутствие теплообмена между отдельными участками жидкости означает, что движение происходит адиабатически. Таким образом, движение идеальной жидкости следует рассматривать как адиабатическое.

          При адиабатическом движении энтропия каждого участка жидкости остаётся постоянной при перемещении последнего в пространстве. Обозначая  S  энтропию, отнесённую к единице массы жидкости, мы можем выразить адиабатичность движения уравнением

.

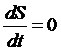          полная производная по времени означает изменение энтропии заданного перемещающегося участка жидкости. Эту производную можно записать в виде

 .

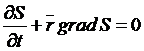          Это есть общее уравнение, выражающее собой адиабатичность движения идеальной жидкости. С помощью уравнения неразрывности его можно написать в виде уравнения неразрывности для энтропии.

 ,

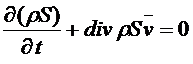          где  - плотность потока энтропии.

          Иногда это условие используют в более простой форме. Если в некоторый момент времени энтропия одинакова во всех точках объёма жидкости, то она остаётся везде одинаковой и неизменной со временем и при дальнейшем движении жидкости.

          В этих случаях уравнение адиабатичности записывается в виде

S=const .

          Изэнтропичностью движения можно воспользоваться и представить уравнения Эйлера в другом виде. Из термодинамических соотношений известно

 ,

где w - тепловая функция единицы массы жидкости, V - удельный объём, Т - температура.

          Поскольку S=const,  имеем просто

,

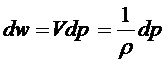          и поэтому

 .

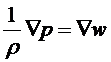          Уравнения Эйлера можно записать в виде

 .

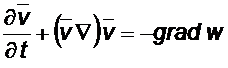          Воспользуемся известной формулой векторного анализа

.

          уравнение Эйлера можно записать в другом виде

 .

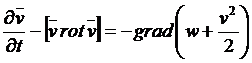          К уравнениям движения необходимо добавить граничные условия, которые должны выполняться на ограничивающих жидкость границах. Для идеальной жидкости это условие должно выражать собой просто тот факт, что жидкость не может проникнуть за твёрдую поверхность.

          На неподвижных стенках это означает, что должна обращаться в нуль нормальная к стенке компонента вектора скорости:

 .