Местные потери напора происходят в так называемых местных гидравлических сопротивлениях, т. е. в местах изменения формы и размеров русла, где поток так или иначе деформируется - расширяется, сужается, искривляется - или имеет место более сложная деформация. Местные потери выражают формулой Вейсбаха: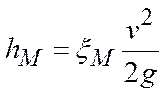 
,
где v — средняя скорость потока в сечении перед местным сопротивлением (при расширении) или за ним (при сужении) н в тех случаях, когда рассматривают потери напора в гидро-арматуре различного назначения; 
безразмерный коэффициент местного сопротивления.
Числовое значение коэффициента в основном определяется формой местного сопротивления, его геометрическими параметрами, но иногда влияет также число Рейнольдса, которое для труб диаметром d выражается формулой
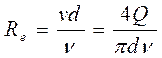
Здесь v — кинематическая вязкость жидкости, выражаемая в м2/с или см2/с. Для некруглых труб Re=(»£>r)/v, где D, — i гидравлический диаметр, равный отношению площади сечения трубы к 1/4 периметра сечения. Число Рейнольдса определяет режим движения жидкостей (и газов) в трубах.
При Re<Reкp, где Reкp
2300, режим движения ламинарный, т. е. слоистый — без перемешивания жидкости и без пульсаций скоростей и давлений.
При Re>Reкp режим течения турбулентный, т. е. с перемешиванием жидкости и с пульсациями скоростей и давлений.
Можно считать, что при турбулентном режиме коэффициенты местных сопротивлений 
от числа Рейнольдса не зависят и,
следовательно потеря напора пропорциональна квадрату скорости (квадратичный режим сопротивления). При ламинарном режиме считают, что
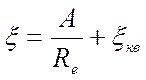
где А — число, определяемое формой местного сопротивления; 
— коэффициент местного сопротивления на режиме квадратичного сопротивления, т. е. при 
При внезапном сужении трубы без закругления коэффициент сопротивления определяют по формуле
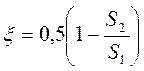
где S1 и S2— площади сечений трубы до и после сужения.
Потери напора на трение по длине / определяются общей формулой Дарси
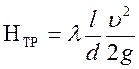
где безразмерный коэффициент сопротивления трения λ определяется в зависимости от режима течения:
при ламинарном режиме 
однозначно определяется число Рейнольдса, т. е.
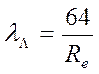
при турбулентном режиме λτ помимо числа Рейнольдса зависит еще от относительной шероховатости Δ/d, т. е.
Распределение скоростей по поперечному сечению круглой трубы радиусом r при ламинарном режиме течения выражается параболическим законом
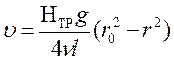
причем максимальная скорость на оси трубы в два раза больше средней.
При ламинарном течении в зазоре 
между двумя плоскими стенками
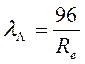
где число Рейнольдса Re — 26υ/ν.
Эtа Формула справедлива также для зазора, образованного двумя соосными цилиндрическими поверхностями при условии, что зазор весьма мал по сравнению с диаметром этих поверхностей. При ламинарном течении в трубке квадратного сечения
.
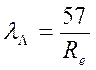Поможем написать любую работу на аналогичную тему