Малое отверстие - отверстие размер которого значительно меньше напора перед отверстием, что позволяет считать давление во всех точках этого отверстия практически одинаковым.
Тонкая стенка - стенка, толщина 
которой не превышает 3d0-где d0-диаметр отверстия.
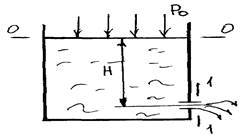На небольшом расстоянии от отверстия(~d0) образуется сжатое сечение, которое имеет min площадь Ас. Степень сжатия оценивается коэффициентом сжатия 
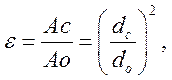(1)
Возьмем сечение у поверхности О-О и сечение 1-1, где струя имеет значение Р1.Запишем уравнение Бернули для сечений:
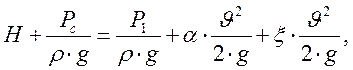где 
– коэффициент сопротивления отверстия. Введем расчетный напор: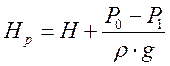 
Тогда расчетный напор: 
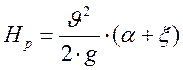. Отсюда определим скорость истечения: 
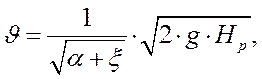(2)
где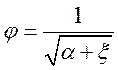 
- коэффициент скорости.
В случае идеальной жидкости: 
Расход жидкости через отверстия:
Истечение жидкости через насадки
Насадки – короткие трубки, присоединенные к отверстию стенки резервуара или к концу трубы.
Для определения скорости истечения и расхода жидкости из насадки применяют те же формулы, что и для малого отверстия в тонкой стенке:(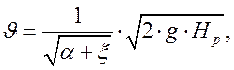
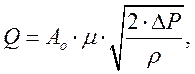), но коэффициенты 
имеют другие значения в зависимости от формы насадки.
Рассмотрим истечение жидкости из резервуара через наружный цилиндрический насадок.
При входе в насадок поток в начале сужается, как и при истечении через отверстие, а затем расширяется заполняя все сечение насадки, т.е. в этом случае Ас=А0, 
.
Поэтому при одинаковом напоре расход жидкости через насадок больше чем через отверстие. Оптимальная длина насадка 
. Если 
, то струя сжимается и истечение происходит аналогично истечению через отверстие. Если 
, то коэффициент потерь 
увеличивается, следовательно, уменьшаются 
и 
.В технике применяют насадки различной
Истечение жидкости через отверстия и насадки при переменном напоре.
Рассмотрим опорожнение открытого в атмосферу конуса произвольной формы через заданное отверстие или насадок с коэффициентом расхода .
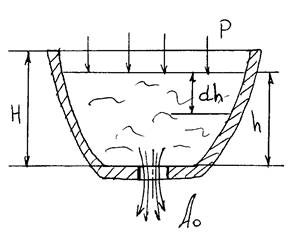
Истечение будет происходить при переменном постепенно уменьшающемся напоре. Обозначим переменную высоту уровня жидкости через h. Площадь сечения резервуара на этом уровне А.
Площадь отверстия А0 . За время dt запишем уравнения объемов:
или 
, (1) где dh-изменение уровня жидкости в сосуде за время dt. «-»-т.е. положительному приращению dt соответствует отрицательное приращение dh.
Время полного опорожнения сосуда высотой Н при 
:
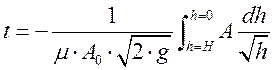(2) Интеграл можно подсчитать, если задан закон изменения площади А по высоте h.
Для призматического сосуда А=const. Тогда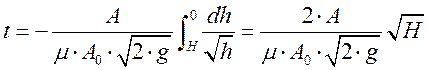 
(3) или
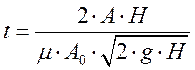(4)
Числитель 
равен удвоенному объему сосуда. Знаменатель
- расход в начальный момент опорожнения, т.е. при напоре Н .
Поможем написать любую работу на аналогичную тему