Простой трубопровод – если он не имеет ответвлений. Они могут быть соединены между собой и образуют последовательное, параллельное соединения и разветвление трубопроводов.
Жидкость движется по трубопроводу благодаря тому, что ее энергия в начале трубопровода меньше чем в конце. Эта разность энергий создается:
1. работой насоса
2. благодаря разности уровней жидкостей
3. давлением газов
Пусть простой трубопровод расположен произвольно. Имеет общую длину L диаметр d и содержит ряд местных сопротивлений.
В сечении 1-1 геометрическая высота = Z1 , а в сечении 2-2 Z2
Скорость потока одинакова и 
. Уравнение Бернулли для сечений 1-1 и 2-2, при 
и исключении скоростных напоров имеет вид:
; 
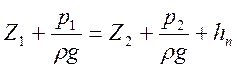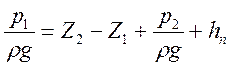(1)
Пьезометрическую высоту 
называют потребным напором
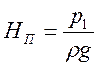если она задана, то она называется располагаемым напором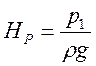 
Обозначим 
, тогда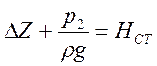 
– статический напор
Слагаемое 
представляем, как степенную функцию расхода 
.
Последовательное соединение трубопроводов
Возьмем несколько трубопроводов различных 
и различных 
содержащих различные местные сопротивления и соединим их последовательно.
При подаче жидкости по такому трубопроводу будет один и тот же, а полная потеря напора между М и N равна сумме потерь во всех трубах.
(1)
(2)
Эти уравнения определяют правила постарения напорных характеристик последовательно соединенных трубопроводов.
Чтобы построить эту напорную характеристику, следует в соответствии с уравнением (2) сложить потери при одинаковых расходах, т.е. сложить ординаты всех трех кривых напорных характеристик при одинаковых абсциссах.
Параллельное соединение трубопроводов.
Это такое соединение трубопроводов 1, 2, 3 между М и N :
Обозначим полные напоры в М и N как 
и 
. Для простоты допускаем, что трубы расположены в горизонтальной плоскости. Расход в основной магистрали ;
Расход в параллельных трубопроводах 
;
Суммарные потери напора в этих трубопроводах 
.
(1)
Потери напора в трубопроводах:
(2)
Потери напора в параллельных трубопроводах равны между собой. В общем случае потери: 
(3)
Следовательно, 
(4)
Система уравнений (1) (4) позволяет решать разные задачи расчета параллельных трубопроводов. Например, задан расход в основной магистрали Q и размеры трубопроводов, а необходимо найти расходы в параллельных трубопроводах Q1 , Q2 , Q3 . Пользуясь уравнениями (1) и (4) можно составить столько уравнений, сколько параллельных трубопроводов между точками М и N.
Из уравнений (1) и (2) следует :
для построения напорной характеристики параллельного соединения трубопроводов следует сложить абсциссы (расходы)
Разветвленное соединение трубопровода.
Разветвленным соединением называется совокупность нескольких простых трубопроводов имеющих одно общее сечение, место разветвления или смыкания.
Пусть основной трубопровод имеет разветвление в сечении М от которого отходит 3 трубы (1,2,3)- разных размеров , содержащие различные местные сопротивления. Геометрическая высота Z1,Z2,Z3 и давления Р1,Р2,Р3 в них также различны. Найдём связь между давлением в сечении N-N и расходами:
.
Также как и для параллельных трубопроводов имеем:
.
Записываем уравнение Бернулли для сечения MN и конечного сечения, например 1 получаем:
.
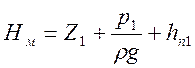Обозначим сумму двух первых членов через :
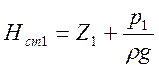
и выразим 3-е слагаемое через расход, получим:
,
аналогично для двух других трубопроводов:
, 
.
Поможем написать любую работу на аналогичную тему