Плоская стенка имеет наклон к горизонтали под углом 
. Вычислим силу
давления действующую со стороны жидкости на некоторый участок стенки, ограниченный произвольным контуром площадью 
. Элементарная сила давления приложена к малой площадке 
будет равна
где 
– давление на свободной поверхности, 
– глубина расположения площадки 
Проинтегрируем полученное выражение по всей площади
cтатический момент площади относительно оси 
, 
– координата площадки . Статический момент площади относительно оси определяют 
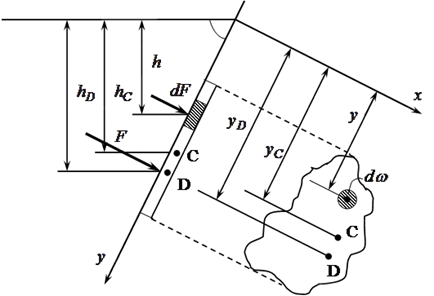Тогда сила 
где 
– глубина расположения центра тяжести площадки .
Таким образом полная сила давления жидкости на плоскую стенку равна произведению площади этой стенки на гидростатическое давление 
в центре масс этой площади. В частном случае, когда является атмосферным и действует также с другой стороны стенки, сила избыточного давления жидкости 
на плоскую стенку равна лишь силе 
давления от веса жидкости. 
В общем случае может существенно отличатся от атмосферного, поэтому полную силу F давления жидкости на стенку рассматривают как сумму 2х сил: 
где 
– сила внешнего давления, – сила от веса жидкости.
Поможем написать любую работу на аналогичную тему