Возьмем точку 
и выделим около нее параллелепипед со сторонами 
. Обозначим внешние силы, отнесенные к единице массы через 
. Внешними силами здесь будут: -объемные, пропорциональные массе параллелепипеда; -силы гидростатического давления, действующие на грани параллелепипеда со стороны окружающей жидкости.
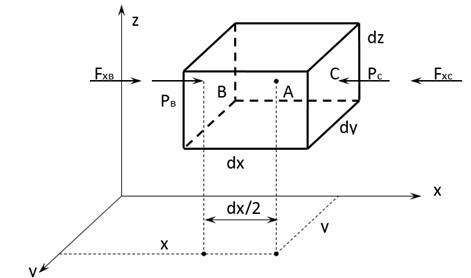
Рассмотрим силы, действующие на жидкий параллелепипед по оси 
.
Проекция объемных сил 
на ось будет равна:
; 
.
Следовательно, проекции объемных сил на все оси:
Гидростатическое давление в точке 
обозначим 
, а в точке С - через 
. Если давление изменяется по линейному закону и непрерывно, тогда:
где 
- градиент гидростатического давления; 
- давление в точке . Силы, действующие на грани равны:
Составим уравнение равновесия исследуемого нами жидкого объема относительно оси : 
Уравнение равновесия после подстановки и преобразования сможем записать в виде: 
Окончательно уравнение равновесия относительно оси будет иметь вид:
Аналогично получим уравнение равновесия относительно осей 
и 
и запишем полную систему уравнений, которые называются уравнениями Эйлера.
Поможем написать любую работу на аналогичную тему