-По месту: внешние и внутренние
-По хар-ру действия: поверхностные(распред по пов-ти объёма силы давлен,вязкости, трения про движен ж-ти, силы поверхностного натяжен)
Массовые(действуют на кажд частицу объёма ж-ти силы веса, инерции, центробежн силы)
Учёт сжимаемости и вязкости ж-ти значит усложняет формульровку и реш-е уравнений движения=>в гидр-ке исп-ют упрощ модели ж-ти
Идеальная ж-ть- невязкая, не сжимаемая ж-ть( иногда сжимаемая).
В гидр массовые силы часто представляют в виде единичн массовых сил.
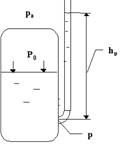Гидростатика-раздел гидравлики, в кот изучаются законы равновесия жидкостей, а так же тел,частично или полностью погружённых в жидкость.
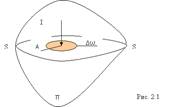Рассмотрим некоторый объем покоящейся жидкости. Выберем внутри него какую-либо точку А и проведем через нее секущую плоскость S-S, которая рассечет объем жидкости на два отсека I и II. Через плоскость S-S на отсек II со стороны отсека I будет действовать сила Р, называемая силой гидростатического давления.
Сила Р будет нормальной силой. Выделим у т. А на поверхности S-S элементарную площадку Й, на которую будет приходиться часть силы Р, которую обозначим Р. Мысленно уменьшая размеры площадки Й, мы получим гидравлическое давление в данной точке, покоящейся жидкости Р, или короче гидростатическое давление
Р=lim Р/Й, (Й’0),или Р=dР/dЙ.
Итак, гидростатическое давление есть предел отношения сжимающей силы Р к элементарной площадке Й при уменьшении размеров последней до 0.
Гидростатическое давление обладает следующими свойствами:
1. Гидростатическое давление действует нормально к площадке действия и является сжимающим, т.е. оно направлено внутрь того объема жидкости, который мы рассматриваем.
2. Гидростатическое давление Р в любой точке одинаково по всем направлениям (т.е. не зависит от угла наклона площадки действия).
Для доказательства этого положения выделим внутри покоящейся жидкости произвольную точку А и выделим у этой точки элементарный объем жидкости в виде прямой призмы (рис. 2.2),в основании которойлежит прямоугольный треугольник АВС.
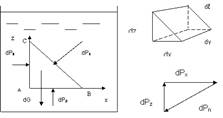
Заменим действие жилкости на призму силами гидростатическоего давления dРх, dРz, dPn, под действием которых призма находится в равновесии. Сила dG-объемная внешняя сила, которой можно пренебречь в силу ее малости.
Т.к. призма находится в равновесии, то треугольник сил будет замкнутым и подобен треугольнику АВС, и тогда из закона подобия следует, что dРх = dPn= dРz или dРх = dPn= dРz
АВ ВС АС d z d d x
Разделим все части этого равенства на длину призмы dy:
dРх = dPn= dРz
dzdy ddy dxdy
В знаменателе каждого из этих выражений площади соответствующих граней призмы. Если размеры dz, dy, d, dx будут стремиться к 0, то в соответствии с выражением для определения гидростатического давления можно записать
px=рn=рz=р.
Следовательно, можно считать, что положение о равенстве давления в одной точке по всем неравенствам доказано.
Давление может быть различно в разных точках жидкости, тоесть является функцией координат р=’(k,y,z),следовательно, функция давления диференциируема и интегрируема.
В единицах СИ давление выражается в паскалях (Па), килопаскалях (кПа). Связь этих единиц с технической атмосферой следующая:
1 кгс/см2=98100 Н/м2=98100 Па=98,1 кПа=0,0981 Мпа
Поможем написать любую работу на аналогичную тему