Задача 8 - Задачи по Гидравлике

Определить работу , затрачиваемую на перемещение поршня площадью Ап=115 мм2 на расстояние L=10 м в трубопроводе соединяющем 2 резервуара площадями А1=0,005 м2 и А2=0,01 м2 заполненных при начальном положении поршня до одной и той же высоте жидкостью =1000 кг/ м3 . Трением поршня о стенки трубопровода пренебречь.

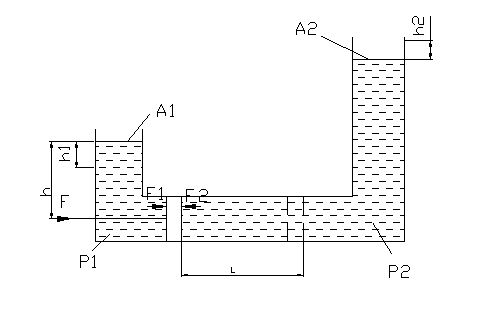
Уравнение равновесия поршня: F+F1-F2=0

F=F1-F2

F1=Ап*Р1=Ап* g(h-h1)

F2=Ап*Р2=Ап*g (h+h2)

h1,h2- изменение уровня жидкости при перемещении поршня на величину L

Уравнение постоянства объемов жидкости при перемещении поршня на величину L.

А1*h1=Aп*L=A2*h2

h1=(Aп/A1)*L              ;                   h2=(Aп/A2)*L

тогда:

F=Aп* g *(h+(Aп/A1)*L)- Aп* g *(h- (Aп/A2)*L)= Aп* g *( (Aп/A1)+ +(Aп/A2))*L

т.е. F переменная

при L=0 F=0    :       L=L F=max

Fmax= Aп* g *( (Aп/A1)+ (Aп/A2))*L

Работа силы F:

W=0.5*Fmax*L=0.5* Aп* g *( (Aп/A1)+ (Aп/A2))*L2=

=0.5*(115*10-)*1000*9.81*102*

*(115*10-6)/0.005+(115*10-6)/0.01)=194.6 Дж