Рисунок
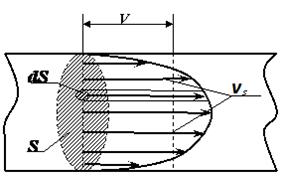
6.3 Распределение скоростей в трубе круглого сечения
Поток идеальной жидкости, можно представить совокупностью элементарных струек жидкости. Скорости по сечению потока неодинаковы, причём в середине потока скорости наибольшие, а к периферии они уменьшаются (струйная модель потока). Это означает, что различные струйки в одном сечении имеют различные значения кинетической энергии. Отсюда следует, что кинетическая энергия, посчитанная с использованием скоростей элементарных струек vS, и кинетическая энергия, посчитанная с использованием значения средней скорости потока V, будет иметь разные значения. Кинетическая энергия элементарной струйки dEэс равна:
где 
‑ масса жидкости плотностью ρ, протекающей через живое сечение элементарной струйки dS со скоростью vS
за время dt, равная:
Проинтегрировав выражение для 
, получим выражение для кинетической энергии потока идеальной жидкости 
.
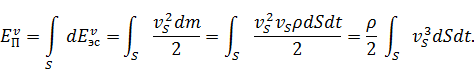
Если принять, что t=1, получим:
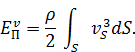
Последняя формула определяет энергию потока с использованием скоростей элементарных струек vS.
Если получить значение кинетической энергии потока с использованием значения средней скорости потока V , получим формулу:
где m ‑ масса жидкости плотностью ρ, протекающей через живое сечение потока S со скоростью V за время t, равная:
После подстановки при t=1 окончательно получим:
Отношение и 
, равное:
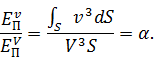
Полученная величина 
называется коэффициентом кинетической энергии или коэффициентом Кориолиса. Смысл этого коэффициента заключается в отношении действительной кинетической энергии потока в определённом сечении к кинетической энергии в том же сечении потока, но при равномерном распределении скоростей. При равномерном распределении скоростей его значение равно единице, а при неравномерном – всегда больше единицы и для любого потока его значение находится в пределах от 1 до 2 и более.
Учитывая коэффициент кинетической энергии, приведём уравнение Бернулли для потока идеальной жидкости, которое примет вид:
Надо учесть, что в общем случае в разных сечениях потока коэффициент будет иметь различные значения.
Поможем написать любую работу на аналогичную тему