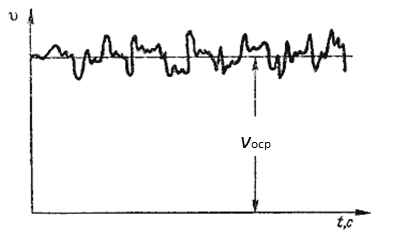
Для турбулентного течения характерно перемешивание жидкости, пульсации скоростей и давлений. Если с помощью особо чувствительного прибора-самописца измерять пульсации, например, скорости по времени в фиксированной точке потока, то получим
Рисунок
7.4 Пульсация скорости в турбулентном потоке
Скорость беспорядочно колеблется около некоторого осредненного по времени значения ![]() , которое в данном случае остается постоянным.
, которое в данном случае остается постоянным.
Характер линий тока в трубе в данный момент времени отличается большим разнообразием (рис.7.5).

Рисунок
7.5 Характер линий тока в турбулентном потоке
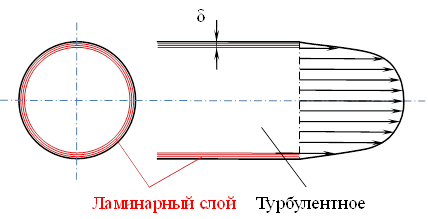
При турбулентном режиме движения жидкости в трубах эпюра распределения скоростей имеет вид.
Рисунок
7.6 Модель турбулентного режима движения жидкости
В тонком слое толщиной ![]() жидкость течет в ламинарном режиме, а остальные слои текут в турбулентном режиме, и называются турбулентным ядром. Таким образом, строго говоря, турбулентного движения в чистом виде не существует. Оно сопровождается ламинарным движением у стенок, хотя слой
жидкость течет в ламинарном режиме, а остальные слои текут в турбулентном режиме, и называются турбулентным ядром. Таким образом, строго говоря, турбулентного движения в чистом виде не существует. Оно сопровождается ламинарным движением у стенок, хотя слой ![]() с ламинарным режимом очень мал по сравнению с турбулентным ядром.
с ламинарным режимом очень мал по сравнению с турбулентным ядром.
Основной расчетной формулой для потерь напора при турбулентном течении жидкости в круглых трубах является эмпирическая формула, называемая формулой Дарси ‑ Вейсбаха:
![]()
Различие заключается лишь в значениях коэффициента гидравлического трения ![]() . Этот коэффициент зависит от числа Рейнольдса
. Этот коэффициент зависит от числа Рейнольдса ![]() и от безразмерного геометрического фактора ‑ относительной шероховатости
и от безразмерного геометрического фактора ‑ относительной шероховатости ![]() (или
(или ![]() , где r0 - радиус трубы).
, где r0 - радиус трубы).
Впервые наиболее исчерпывающей работы по определению были даны И.И. Никурадзе, который на основе опытных данных построил график зависимости lg(1000λ) от lg
![]() для ряда значений
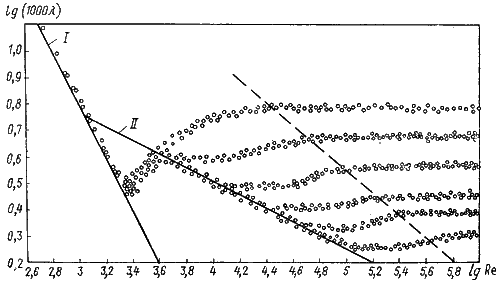
для ряда значений ![]() . Опыты Никурадзе были проведены на трубах с искусственно заданной шероховатостью, полученной путем приклейки песчинок определенного размера на внутренние стенки трубопровода. Результаты этих исследований представлены на графике Никурадзе,
. Опыты Никурадзе были проведены на трубах с искусственно заданной шероховатостью, полученной путем приклейки песчинок определенного размера на внутренние стенки трубопровода. Результаты этих исследований представлены на графике Никурадзе,
Рисунок
7.7 График Никурадзе
где построены кривые зависимости ![]() от
от ![]() для ряда значений
для ряда значений ![]() .
.
Прямая I соответствует ламинарному режиму движения жидкости.
Далее на графике можно рассматривать три области.
Первая область - область малых ![]() и
и ![]() , где коэффициент
, где коэффициент ![]() не зависит от шероховатости, а определяется лишь числом
не зависит от шероховатости, а определяется лишь числом ![]() (отмечена на рис.7.7 прямой II). Это область гидравлически гладких труб. Если число Рейнольдса лежит в диапазоне 4000 < Re < 10(
(отмечена на рис.7.7 прямой II). Это область гидравлически гладких труб. Если число Рейнольдса лежит в диапазоне 4000 < Re < 10(![]() ) коэффициент
) коэффициент ![]() определяется по полуэмпирической формуле Блазиуса
определяется по полуэмпирической формуле Блазиуса
![]()
Для определения существует также эмпирическая формула П.К. Конакова, которая применима для гидравлически гладких труб
![]()
Во второй области, расположенной между линий II и пунктирной линией справа, коэффициент ![]() зависит одновременно от двух параметров ‑ числа
зависит одновременно от двух параметров ‑ числа ![]() и относительной шероховатости
и относительной шероховатости ![]() , которую можно заменить на Δэ. Для определения коэффициента
, которую можно заменить на Δэ. Для определения коэффициента ![]() в этой области может служить универсальная формула А.Д. Альтшуля:
в этой области может служить универсальная формула А.Д. Альтшуля:
![]()
где Δэ - эквивалентная абсолютная шероховатость.
Характерные значения Δэ (в мм) для труб из различных материалов приведены ниже:
|
Стекло |
0 |
|
Трубы, тянутые из латуни, свинца, меди |
0…0,002 |
|
Высококачественные бесшовные стальные трубы |
0,06…0,2 |
|
Стальные трубы |
0,1…0,5 |
|
Чугунные асфальтированные трубы |
0,1…0,2 |
|
Чугунные трубы |
0,2…1,0 |
Третья область - область больших ![]() и Δ/r0, где коэффициент
и Δ/r0, где коэффициент ![]() не зависит от числа
не зависит от числа ![]() , а определяется лишь относительной шероховатостью (область расположена справа от пунктирной линии). Это область шероховатых труб, в которой все линии с различными шероховатостями параллельны между собой. Эту область называют областью автомодельности или режимом квадратичного сопротивления, т.к. здесь гидравлические потери пропорциональны квадрату скорости.
, а определяется лишь относительной шероховатостью (область расположена справа от пунктирной линии). Это область шероховатых труб, в которой все линии с различными шероховатостями параллельны между собой. Эту область называют областью автомодельности или режимом квадратичного сопротивления, т.к. здесь гидравлические потери пропорциональны квадрату скорости.
Определение ![]() для этой области производят по формуле Шифринсона:
для этой области производят по формуле Шифринсона:
![]()
или по формуле Прандтля - Никурадзе:
![]()
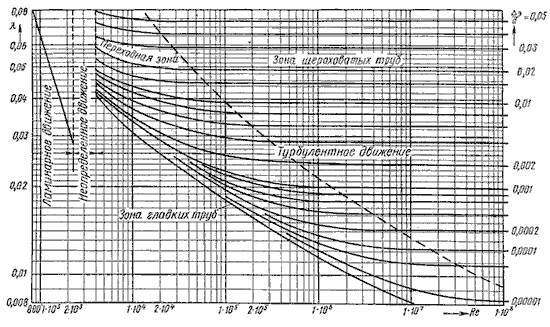
Итак, потери напора, определяемые по формуле Дарси ‑ Вейсбаха, можно определить, зная коэффициент гидравлического сопротивления, который определяется в зависимости от числа Рейнольдса ![]() и от эквивалентной абсолютной шероховатости Δэ. Пользоваться данными формулами для определения коэффициента λ не всегда удобно. Для облегчения расчетов можно пользуются номограммой Колбрука-Уайта (рис.8), при помощи которой по известным
и от эквивалентной абсолютной шероховатости Δэ. Пользоваться данными формулами для определения коэффициента λ не всегда удобно. Для облегчения расчетов можно пользуются номограммой Колбрука-Уайта (рис.8), при помощи которой по известным ![]() и Δэ/ d очень просто определяется
и Δэ/ d очень просто определяется ![]() .
.
Рисунок
7.8 Номограмма Колбрука-Уайта для определения коэффициента гидравлического трения
Поможем написать любую работу на аналогичную тему

