Физическая модель отличается от натуры лишь размерами, т.е. модель по своим размерам может быть, чаще всего лишь уменьшенной копией натуры, либо она может (в некоторых случаях) превосходить по своим размерам натуру. И в том и другом случае, для успешного и правильного построения модели необходимо, прежде всего, знать основные законы подобия. Модель и натура будут адекватны между собой, если при построении модели будут выполнены все основные элементы подобия. К таким условиям относятся критерии геометрического, кинематического и динамического подобия.
Для геометрического подобия необходимо, чтобы отношение любых сопоставляемых линейных размеров модели и натуры были бы одинаковыми. Так протяжённость модели и натуры, а также и другие прочие размеры должны находится между собой в пропорциональной зависимости:
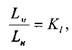
где: 
и 
- линейный размер соответственно на модели и на натуре,
- коэффициент геометрического подобия, масштаб моделирования.
В таком случае, при сопоставлении размеров площадей на модели и натуре должен соблюдаться такой же масштабный множитель, но с учётом порядка мерности величины:
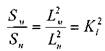
Т.е. при сопоставлении размеров площадей на модели и на натуре соотношение этих величин будет равно квадрату масштабного линейного множителя. Соответственно для сопоставления объёмов:
Для кинематического подобия необходимо, чтобы траектории всех сопоставимых частиц были геометрически подобны, т.е. при этом кроме геометрического подобия сопоставимых криволинейных отрезков модели и натуры выполнялось ещё подобие сопоставимых интервалов временни в моделе и натуре.
Тогда величины скоростей движения частиц в модели и натуре будут относиться между собой как:
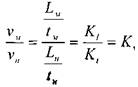5 - величины расходов жидкости: '
Для динамического подобия сравниваемых потоков необходимо, чтобы в соответствующих местах потоков были подобны действующие в них одноимённые силы. Пусть в сопоставимых точках потока жидкости и строящейся модели этого потока действует некоторая инерциальная сила F. Тогда при соблюдении геометрического и кинематического подобия, критерий динамического подобия может быть выражен следующим образом:
Величина
носит название масштаба сил.
Рассмотрим критерии подобия отдельных сил действующих в жидкости.
Сила внутреннего трения в жидкости.
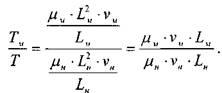
Заменив 
мы получим основное условие подобия потоков, в которых ос-
новную роль играют силы внутреннего трения жидкости. Для подобия таких потоков необходимо равенство чисел Рейнольдса.
Определяющей в потоке является сила тяжести.
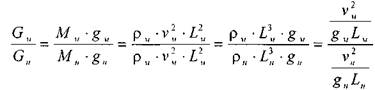j
Таким образом, если определяющей силой в потоке является сила тяжести, то для подобия таких потоков необходимо постоянство числа Фруда
Для потока жидкости, в котором определяющей силой является сила давления:
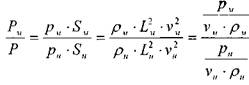
Если определяющей в потоке жидкости является сила давления, то для подобия таких потоков обязательным условием является равенство критерия Эйлера
Поможем написать любую работу на аналогичную тему