Два подхода к описанию движения сплошной среды. Переменные Эйлера и Лагранжа

          Для описания движения сплошной среды возможны два подхода. Один из них называется лагранжевым, другой - эйлеровым.

          Лагранжев метод описания движения относится к типу отсчётных. В некоторый (начальный) момент времени t0 каждая из жидких частиц маркируется путём присвоения ей значения координат в данный момент времени.

          В трёхмерном пространстве введём обозначения

.

          В дальнейшем прослеживается движение каждой частицы индивидуально. При таком подходе положение частицы в каждый момент времени  будет зависеть от параметров a, b, c и t, которые называются переменными Лагранжа. Можно записать, что вектор положения жидкой частицы равен

.

          Скорость жидкой частицы выразится через производную радиус-вектора

,

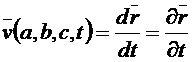а ускорение через производную скорости

.

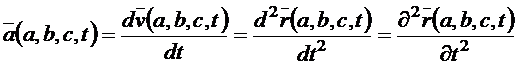          В последних двух формулах при дифференцировании параметры a, b, c являются постоянными,  и являются только функционалами времени и в этом случае энергии дифференцирования  и  тождественны.

          Эйлеров метод описания движения относится к типу пространственных. В каждой точке пространства с координатами x,y,z изучаются параметры движения в различные моменты времени t. Таким образом, скорость жидкости в различных точках пространства должна быть функцией четырёх переменных x, y, z, t , называемых переменными Эйлера,

,

а её дифференциал

.

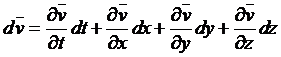В движущейся среде приращения  не являются независимыми, а соответственно равны

.

     Поэтому справедливо равенство

,

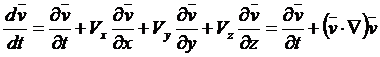  где   .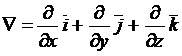

          Это означает, что полное ускорение    индивидуальной жидкой частицы, находящейся в момент времени t в точке пространства с координатами x,y,z, состоит из двух частей: локального ускорения , обусловленного изменением скорости во времени в данной точке, и конвективного ускорения, обусловленного неоднородностью поля скоростей в окрестности данной точки и связанного с этим обстоятельством конвективного переноса.

          Производная  носит название индивидуальной или субстанциональной производной.

          Если =0, поле скоростей стационарно, однако это ещё не означает, что в жидкости отсутствуют ускорения. Стационарность или нестационарность поля скоростей зависит от выбора системы координат.

Если = 0, то поле скоростей однородно.