Молекулы жидкости, находящиеся на свободной поверхности (границе раздела жидкость - газ или жидкость - пар), испытывают одностороннее воздействие со стороны соседних молекул. Поэтому на криволинейной поверхности должны возникать растягивающие усилия. Для количественного описания этого явления ещё в 1805 году Юнгом была проведена классическая аналогия с упругой плёнкой. Натяжение этой плёнки, т.е. усилие, приходящееся на единицу длины поперечного разреза плёнки, характеризуется коэффициентом поверхностного натяжения
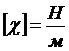 .
.
Сила поверхностного натяжения стремится сократить площадь свободной поверхности. Их действие впервые обнаружено в капиллярах, поэтому эти силы до сих пор часто называют капиллярными.
Величина ![]() зависит прежде всего от природы контактирующих сред. Числовые значения его для некоторых пар приведены в таблице 5.
зависит прежде всего от природы контактирующих сред. Числовые значения его для некоторых пар приведены в таблице 5.
Таблица 5
|
Вещество |
Контактирую-щая среда |
Температура, К |
Коэффициент поверхностного натяжения, |
|
Вода |
Воздух |
293 |
78.2 |
|
Вода |
Воздух Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
|
373 |
58.8 |
|
Жидкий водород |
Пар вещества |
21 |
20 |
|
Жидкий кислород |
Пар вещества |
91 |
13.0 |
Коэффициент поверхностного натяжения ![]() падает с ростом температуры и практически не зависит от давления. Поверхностное натяжение может быть существенно снижено с помощью поверхностно-активных веществ, к числу которых относятся моющие средства.
падает с ростом температуры и практически не зависит от давления. Поверхностное натяжение может быть существенно снижено с помощью поверхностно-активных веществ, к числу которых относятся моющие средства.
Величина ![]() может служить мерой свободной энергии, которой обладает граница раздела:
может служить мерой свободной энергии, которой обладает граница раздела:
![]() ,
,
где ![]() - площадь свободной поверхности.
- площадь свободной поверхности.
В этом случае
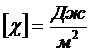 ,
,
что согласуется с ранее указанной размерностью.
Существование поверхностного натяжения должно приводить к возникновению на криволинейной поверхности перепада давлений, которые будут зависеть от конкретной геометрии поверхности.
Для объяснения этого факта рассмотрим равновесие элемента неплоской поверхности с линейными размерами ![]() и
и ![]() и главными радиусами кривизны R1 и R2 соответственно ( рис. 7).
и главными радиусами кривизны R1 и R2 соответственно ( рис. 7).
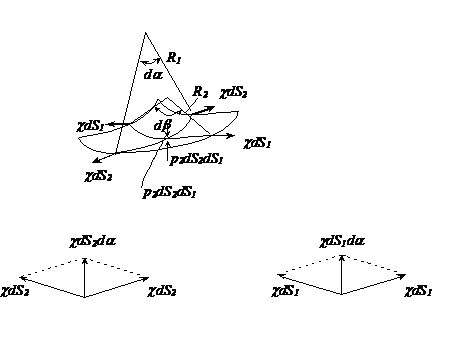
Рис. 7
Равнодействующие сил поверхностного натяжения, действующих на границе выделенного контура, равны cdS2 и cdS1, а возникающая вследствие этого сила, действующая по нормали к выделенной площадке, в первом приближении равна
![]() .
.
С учётом того, что
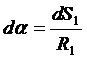 и
и 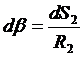 ,
,
имеем выражение для силы
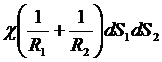 .
.
Эта величина, очевидно, и есть скачок давления на поверхности раздела двух сред, обусловленный поверхностным натяжением.
Обозначив теперь через p1 и p2 давление в средах на границе раздела из условия равновесия элементарной площадки, запишем соотношение
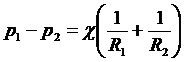 ,
,
которое называется формулой Лапласа.
Для цилиндрических поверхностей с круговым поперечным сечением радиуса R имеем ![]() ,R2=R и формула Лапласа принимает вид:
,R2=R и формула Лапласа принимает вид:
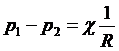 .
.
В случае сферических поверхностей R1=R2=R и тогда получаем:
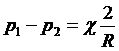 .
.
Если радиус сферической полости мал, то давления, развиваемое поверхностным натяжением, могут стать значительными.
|
Рис. 8 |
Весьма характерной является система газ - жидкость – твёрдая стенка ( рис. 8). В этом случае вводят значение краевого угла ( угла контакта или угла смачивания). Характерные значения краевых углов приведены в таблице 6. Если |
Таблица 6
|
Твёрдое вещество |
Жидкость |
Краевой угол, град. |
||
|
Сталь |
Вода |
70 - 90 |
||
|
Сталь |
Жидкий водород |
0 |
||
|
Сталь |
Жидкий кислород |
0 |
||
|
Стекло |
Ртуть |
128-148 |
||
|
Рис. 9 |
Высота подъёма или опускания жидкости в капилляре определяется с помощью соотношения
где d- диаметр капилляра, а q - угол смачивания ( рис. 9 ).
|
|
|||
Поможем написать любую работу на аналогичную тему



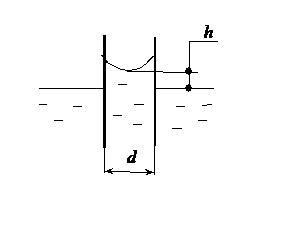
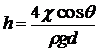 ,
,