В отличие от классических психофизических методов в современной психофизике особое внимание уделяется тому, как и почему человек дает тот или иной ответ, обнаруживая слабый пороговый сигнал или оценивая пороговые различая между двумя сигналами. Для описания поведения человека-наблюдателя, решающего сенсорную пороговую задачу, строится специальная модель. Новая методология, называемая психофизической теорией обнаружения сигнала, или ТОС , содержит в себе представление о наблюдателе не как о пассивном приемнике стимульной информации, но как об активном субъекте принятия решения в ситуации сенсорной неопределенности.
Общая схема, предлагаемая ТОС для описания процесса обнаружения порогового сигнала (или порогового различения двух сигналов), проста: 1) последовательность стимульных воздействий отображается в сенсорной системе в виде множества ощущений, и этот процесс имеет вероятностную природу, т.е. одно и то же стимульное воздействие вызывает каждый раз немного отличающуюся интенсивность ощущения данного сенсорного качества;
2) в силу высокой сенсорной неопределенности, обусловленной малой интенсивностью ощущения от воздействия порогового сигнала, наблюдатель каждый раз с достаточной уверенностью не может определить, был или не был сигнал, но тем не менее в соответствии с инструкцией вынужден принимать определенное решение, основываясь не только на сенсорной информации, но с учетом своих ожиданий, прошлого опыта или пытаясь угадать.
Таким образом, сенсорный процесс описывается как двухступенчатый: процесс отображения физической энергии стимула в интенсивность ощущения и процесс принятия решения. В ТОС не используется понятие сенсорного порога, поскольку наблюдатель может и на основе достаточно интенсивного ощущения решить, что сигнала он не почувствовал (например, не ожидая сигнала в данной пробе) или, наоборот, имея очень слабое ощущение стимульного воздействия, сказать «да», если это воздействие представляется ему очень вероятным.
Для разработки методов оценки сенсорной чувствительности в рамках ТОС строится формальная модель, описывающая поведение наблюдателя, решающего сенсорную задачу. Та часть модели, которая представляет процесс отображения энергии стимула во множество ощущений, взята из статистической радиофизики, другая часть, рассматривающая правила принятия решения, пришла из математической теории решений.
Рассмотрим метод «да-нет» как один из самых популярных методов измерения сенсорной чувствительности, разработанный в рамках ТОС. В отличие от классической психофизики мы уже не измеряем абсолютный или разностный порог, а говорим об измерении сенсорной чувствительности в задаче обнаружения сигнала или в задаче различения сигналов. В этом методе используются только два стимула, незначительно отличающиеся по интенсивности
некоторого физического качества: один «значащий» — <C>, и другой «пустой» — <Ш>1. Предъявления следуют друг за другом обыкновенно через более или менее регулярные интервалы времени, и после каждого предъявления испытуемый отвечает «да», если ему показалось, что был сигнал, или «нет», если он не обнаружил сигнала. Стимулы предъявляются в опыте много раз в случайном порядке.
Рассмотрим теперь возможные комбинации <предъявление — ответ>, которые могут встретиться в опыте. Их четыре: <С — да>, <Ш — нет>, <С — нет>, <Ш — да>, причем первые два сочетания являются правильными, два последних — ошибочными исходами.
Каждое их этих сочетаний имеет свое специальное название (табл. 1). Попадание и ложная тревога будут в дальнейшем обозначаться через H (от англ. hit) и .A (от англ. false alarm). Обозначения для пропусков — O (omission) и правильных отрицаний — CR (correct rejection).
Чтобы охарактеризовать деятельность испытуемого в данном опыте, принято представлять результаты эксперимента в виде оценок условных вероятностей — вероятностей того, что испытуемый ответит правильно (неправильно) при условии, что был предъявлен определенный стимул — значащий или пустой. Такие вероятности обозначаются так: P (да/С), P (да/Ш), P (нет/С), P (нет/Ш). В частности, первая из этих вероятностей есть вероятность правильного обнаружения сигнала, а вторая — вероятность ложной тревоги. Если вычислены две эти условные вероятности, вычисление двух остальных уже не требуется. Они не несут дополнительной информации, так как
Эта пара вероятностей полностью характеризует успешность обнаружения сигнала наблюдателем.
Как было сказано выше, воздействия стимулов связаны со своими сенсорными репрезентациями случайно или стохастически.
В ТОС эта связь изображается в виде двух перекрывающихся функций плотности вероятности нормального распределения (рис. 29)1. Особо подчеркнем, что на этой модельной картинке ось абсцисс —это гипотетическая ось интенсивности ощущений, которые появлялись в опыте при действии значащего (правое распределение) и пустого (левое распределение) стимулов.
Их перекрытие означает, что сенсорные репрезентации <С> и <Ш> оказываются похожими друг на друга, и наблюдатель не может каждый раз со 100-процентной уверенностью решить, какой же стимул был ему предъявлен. Далее в модели предполагается, что при принятии решения наблюдатель устанавливает строго определенное правило соответствия между своими ощущениями и двумя типами ответов («да» и «нет») и всегда ему следует: если текущее ощущение имеет интенсивность выше некоторого критического уровня, то он говорит «да», если меньше — «нет»1. Таким образом, в ТОС вводится понятие критерия принятия решения наблюдателя о наличии/отсутствии значащего стимула. Фактически критерий — это некоторый сенсорный образ памяти, или сенсорный эталон, с которым сравнивается каждая сенсорная репрезентация (см. точку С на оси абсцисс рис. 29). Его положение на сенсорной оси (оси абсцисс) может зависеть от целого ряда причин: субъективные веса различных ошибок (например, наблюдатель может стараться минимизировать число пропусков и не очень заботиться об уменьшении числа ложных тревог), знания объективной вероятности предъявления значащих и пустых проб в опыте, использование экспериментатором системы «выплат» и «штрафов», соответственно, за верные и ложные ответы, в денежной или игровой форме (так называемая платежная матрица — ПМ) и т.д.
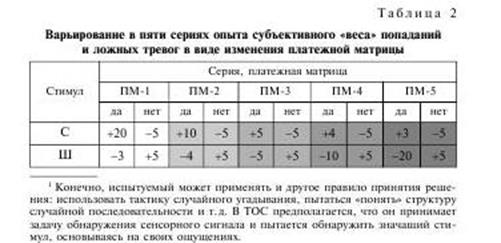
Например, посмотрим, как изменит положение своего критерия принятия решения типичный испытуемый в случае использования в опыте по обнаружению порогового сигнала пяти разных платежных матриц, соответствующих пяти различным способам оплаты за правильные ответы и штрафам за неправильные
(числа обозначают рубли — табл. 2). Пусть ему в каждой из пяти серий будет предъявлено по 100 значащих и пустых проб.
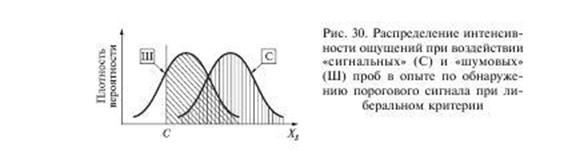
Очевидно, что в первой серии испытуемому выгодно в случае сомнения давать ответ «да»: в случае правильного ответа он получает 20 руб., в случае неправильного — его штрафуют всего лишь на 3 руб. При такой платежной матрице говорят, что у испытуемого формируется либеральный критерий, при использовании которого в задаче обнаружения порогового сигнала среди ответов испытуемого будет много попаданий, но и много ложных тревог.
Иные условия в V серии: за каждую ложную тревогу налагается штраф в 20 руб., а за правильное обнаружение сигнала платят всего 3 руб. Оптимальная стратегия в данном случае заключается в
том, чтобы очень аккуратно использовать ответы «да», лишь в тех пробах, когда ощущение о наличии сигнала было достаточно сильным. При сомнении выгоднее давать ответы «нет»: выиграешь немного, но зато и при знании реальной пропорции значимых и пустых проб — мало проиграешь. При такой платежной матрице говорят об использовании строгого критерия (рис. 31).
В экспериментах строгость критерия изменяется не только платежной матрицей, но и путем изменения априорной вероятности предъявления значащего сигнала в каждой серии. Этот прием также формирует у испытуемого закономерную систему ожиданий: он знает, что при вероятности 90 % из 100 проб 90 будут содержать «значащий» стимул и только 10 — «пустой»; при вероятности 10 % — все наоборот: 90 «пустых» и только 10 «значащих».
Естественно ожидать, что в первом случае у испытуемого формируется либеральный, а во втором — строгий критерий принятия решения. Таким образом, изменяя величину априорной вероятности появления значащего сигнала в ряде проб от 0 до 100 % можно направленно изменять строгость критерия принятия решения.
Понятно, что такая ситуация, описываемая ТОС, возникает лишь в случае незначительных (пороговых) физических различий между <С> и <Ш>, а следовательно при большом сходстве ощущений, возникающих в ответ на эти стимулы. Очевидно, что данная ситуация соответствует поведению человека в условиях высокой сенсорной неопределенности, когда при явном дефиците информации необходимо тем не менее принимать решение.
Положение критерия принятия решения однозначно определяет пару чисел Р(.A) и Р(H ), которые мы получаем в результате проведения опыта по обнаружению пороговых различий между <С> и <Ш>. Каждой паре чисел можно поставить в соответствие точку внутри квадрата (рис. 32), на вертикальной стороне которого откладывается Р(H ), а на горизонтальной — Р(.A), и, таким образом, наглядно представить результат работы наблюдателя с использованием различных критериев принятия решения (например, предлагая ему пять разных платежных матриц — ПМ). Полученная по этим точкам кривая (на рис. 32 она показана состоящей их отдельных точек, полученных в отдельных сериях опыта) называется рабочей характеристикой наблюдателя или просто — PX.

![]()

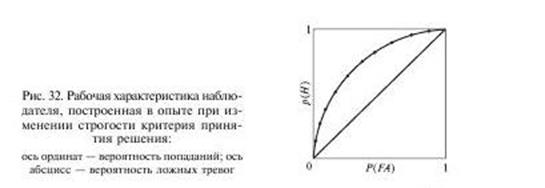
Вероятности Р(H ) и Р(.A) меняются содружественно, т.е. нельзя только путем изменения критерия одновременно увеличить одну из них и уменьшить другую. Это очень важное положение ТОС верно для любых пар f(X/С) и f(X/Ш). Из него следует, что только пара этих вероятностей, а не каждая в отдельности, характеризует сенсорную способность наблюдателя. PX идет из точки (0,0) квадрата в точку (1,1) и при этом располагается выше его главной диагонали. Последнее следует из того, что распределение f(X/С) сдвинуто вправо относительно f(X/Ш), т.е. Р(H ) всегда превышает Р(.A), когда наблюдатель действительно различает сенсорные образы сигнального и шумового стимулов. Чем выше сенсорная чувствительность наблюдателя, тем более выпукла РХ и тем ближе она к левому верхнему углу квадрата (рис. 33). Понятно, что на диагонали располагаются точки, имеющие одинаковые значения пропорций попаданий и ложных тревог, т.е. соответствующие нулевому уровню чувствительности.
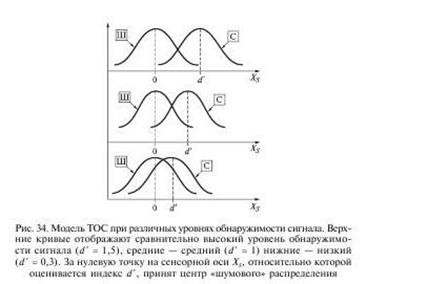
В ТОС вводится особая мера сенсорной чувствительности — индекс dґ, как расстояние на горизонтальной оси (рис. 34) между центрами двух распределений f(X/С) и f(X/Ш). dґ рассчитывается следующим образом1:
dґ = z(H) − z(.A), (15)
где z(H) и z(.A) — величины вероятностей попаданий и ложных тревог, преобразованные в единицы стандартного отклонения по таблице нормального распределения.
Также вводится мера строгости критерия принятия решения, так называемое отношение правдоподобия, или β. Этот индекс рассчитывается по специальным таблицам как отношение ординаты «сигнального» распределения f(X/С) к ординате «шумового» распределения f(X/Ш) в точке С. Кроме того, можно непосредственно вычислить положение точки С на оси абсцисс:
C = −0,5. (16)
Два этих индекса (dґ и β) являются надежными оценками сенсорной чувствительности и критерия лишь при принятии двух основных математических предположений ТОС: нормальности и равновариативности2 распределений сенсорных эффектов f(X/С) и f(X/Ш). В реальной экспериментальной практике, чтобы не проверять справедливость данных допущений наиболее часто используют непараметрические индексы чувствительности и критерия — Aґ и YesRate, соответственно:
Аґ = 0,5 + (P(H) − P(.A))(1 + P(H) − P(.A))/
/4P(H)(1 − P(.A)). (17)
где Р(«да») — частота ответов «да».
В рамках ТОС были разработаны еще два других метода измерения сенсорной чувствительности: метод двухальтернативного вынужденного выбора (2АВВ) и метод оценки уверенности. Они также широко используются в исследовательской практике.

Поможем написать любую работу на аналогичную тему

