Для более наглядного представления результатов анализа рекомендуется представлять их в графической форме. Для этого используются круговые и векторные диаграммы.
Круговая диаграмма позволяет ответить на вопрос: какова доля влияния отдельных факторов на показатель? Ответ на такой вопрос может быть получен только в случае, когда действия всех факторов однонаправленны, то есть все факторы одновременно или увеличивают, или уменьшают показатель. Влияние каждого из них изображается в виде сектора круга. Сумма всех секторов (площадь круга) - совместное влияние всех факторов на изменение показателя. Доля площади сектора в площади круга характеризует удельный вес влияния изменения фактора на изменения показателя.
Пример 1.8. Изменение цен увеличило выручку от реализации продукции на 1600 тыс.тг., а изменение физического объема реализации увеличило выручку на 6400 тыс.тг.. Определим процентное влияние факторов и изобразим его в виде диаграммы.
Общее изменение выручки
1600+6400=8000 тыс.тг.
Доля влияния цен 1600/8000 *100%=20%.
Доля влияния объемов
6400/8000 *100%=80%.
Соответствующая диаграмма представлена на следующем рисунке.
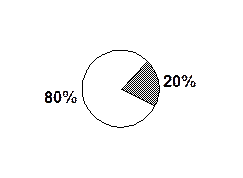
Однако в случае разнонаправленного влияния факторов на динамику показателя решить задачу способом, указанным выше, не удается. Не удается определить процентное участие динамики фактора в динамике показателя. Невозможно построить и круговую диаграмму.
Наиболее удачным способом графического изображения влияния динамики факторов на динамику показателя в общем случае является векторная диаграмма. Она строится на плоскости XоY. На оси oX откладываются отрезки (произвольной длины) для каждого фактора и результирующего показателя. На оси oY указывается масштаб изменения факторов и показателя.
Величина изменения результирующего показателя под воздействием изменения конкретного фактора указывается в виде вектора. Длина вектора равна величине изменения результирующего показателя. Направление - вверх, если изменение положительно, или вниз если изменение отрицательно.
Построение диаграммы может начинаться с изображения влияния любого фактора. Порядок их следования безразличен. Каждый последующий вектор откладывается от конца предыдущего вверх или вниз в зависимости от знака. Начало первого вектора лежит на оси оX.
Вектор, соединяющий ось оX с концом вектора, относящегося к последнему фактору, и будет характеризовать изменение показателя под воздействием всех факторов. Если он направлен вверх изменение показателя положительно, если вниз - отрицательно. Модуль (длина) этого вектора равен суммарной величине изменения результирующего показателя.
Пример 1.9. Показатель является абстрактной функцией трех факторов y = x1 * x2 * х3. Данные о динамике факторов представлены в таблице 1.4.
Таблица 1.4
|
Фактор |
Базисное значение |
Отчетное значение |
|
X1 |
3 |
2 |
|
X2 |
5 |
7 |
|
Х3 |
4 |
3 |
Факторный анализ приращения показателя выполним с использованием, например, метода дифференцирования: Dy = Dx1 * x2 * х3 + x1 * Dx2 * х3 + x1 * x2 *D х3 = (2 - 3)*5*4 + 3*(7 - 5)*4 + 3*5*(3 - 4) = -20 + 24 - 15 = - 11.
Таким образом, изменение показателя вследствие динамики отдельных факторов составит:
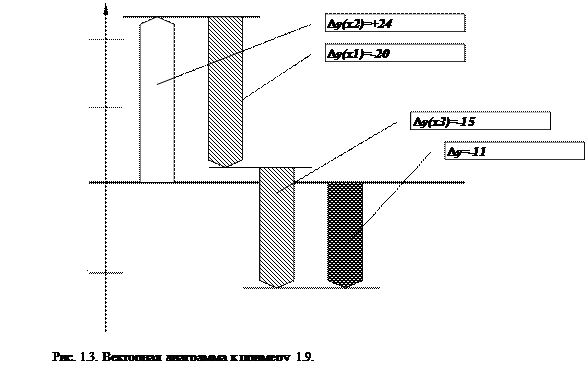
- первого фактора Dy(x1 ) = - 20,
- второго фактора Dy(x2 ) = + 24,
- третьего фактора Dy(х3 )= - 15,
- совместное влияние всех факторов Dy = - 11.
Построение векторной диаграммы начнем, например, со второго фактора. Результат построения изображен на рисунке 1.3.
Поможем написать любую работу на аналогичную тему

