Одним из характерных проявлений жизни является удивительная способность живых организмов кинетически регулировать химические реакции, подавляя стремление к достижению термодинамического равновесия. Ферментативная кинетика занимается исследованием закономерностей влияния химической природы реагирующих веществ (ферментов, субстратов) и условий их взаимодействия (концентрация, рН среды, температуры, присутствие активаторов или ингибиторов) на скорость ферментативной реакции. Главной целью изучения кинетики ферментативных реакций является получение информации, которая может способствовать выяснению молекулярного механизма действия фермента.
Общие принципы кинетики химических реакций применимы и к ферментативным реакциям. Известно, что любая химическая реакция характеризуется константой термодинамического равновесия. Она выражает состояние химического равновесия, достигаемого системой, и обозначается Кр. Так, для реакции:
![]()
Константа равновесия равна произведению концентраций образующихся веществ, деленному на произведение концентрации исходных веществ. Значение константы равновесия обычно находят из соотношения констант скоростей прямой (k+1) и обратной (k–1 ) реакций, т.е. Кp = k+1/k–1. В состоянии равновесия скорость прямой реакции: v+1 = k+1• равна скорости обратной реакции: v–1 = k – 1 • , т. е. v+1 = v–1 соответственно k+1• = k–1•, или
![]()
Таким образом, константа равновесия равна отношению констант скоростей прямой и обратной реакций. Величину, обратную константе равновесия, принято называть субстратной константой, или, в случае ферментативной реакции, константой диссоциации фермент–субстратного комплекса, и обозначать символом KS. Так, в реакции
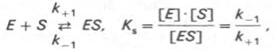
т.е. KS равна отношению произведения концентрации фермента и субстрата к концентрации фермент-субстратного комплекса или отношению констант скоростей обратной и прямой реакций. Следует отметить, что константа KS зависит от химической природы субстрата и фермента и определяет степень их сродства. Чем ниже значение KS, тем выше сродство фермента к субстрату.
При изучении кинетики ферментативных реакций следует учитывать одну важную особенность этих реакций (не свойственную обычным химическим реакциям), связанную с явлением насыщения фермента субстратом. При низкой концентрации субстрата зависимость скорости реакции от концентрации субстрата (рис. 17) является почти линейной и подчиняется кинетике первого порядка. Это означает, что скорость реакции S —> Р прямо пропорциональна концентрации субстрата S и в любой момент времени t определяется следующим кинетическим уравнением:
![]()
где – молярная концентрация субстрата S; –d/dt – скорость убыли субстрата; k' – константа скорости реакции, которая в данном случае имеет размерность, обратную единице времени (мин–1 или с–1).
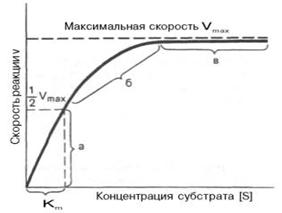
а - реакция первого порядка (при < Кm скорость реакции пропорциональна концентрации субстрата); б - реакция смешанного порядка; в - реакция нулевого порядка, когда v = Vmaxи скорость реакции не зависит от концентрации субстрата
Рисунок 17 - Теоретический график зависимости скорости ферментативной реакции от концентрации субстрата при постоянной концентрации фермента
При высокой концентрации субстрата скорость реакции максимальна, становится постоянной и не зависящей от концентрации субстрата . В этом случае реакция подчиняется кинетике нулевого порядка v = k" (при полном насыщении фермента субстратом) и целиком определяется концентрацией фермента.
Изучая явление насыщения, Л. Михаэлис и М. Ментен разработали общую теорию ферментативной кинетики. Они исходили из предположения, что ферментативный процесс протекает в виде следующей химической реакции:
![]()
т.е. фермент Е вступает во взаимодействие с субстратом S с образованием промежуточного комплекса ES, который далее распадается на свободный фермент и продукт реакции Р. Математическая обработка на основе закона действующих масс дала возможность вывести уравнение, названное в честь авторов уравнением Михаэлиса–Ментен, выражающее количественное соотношение между концентрацией субстрата и скоростью ферментативной реакции:
![]()
где v – наблюдаемая скорость реакции при данной концентрации субстрата ; KS– константа диссоциации фермент-субстратного комплекса, моль/л; Vmax– максимальная скорость реакции при полном насыщении фермента субстратом.
Из уравнения Михаэлиса–Ментен следует, что при высокой концентрации субстрата и низком значении KS скорость реакции является максимальной, т.е. v = Vmax(реакция нулевого порядка, см. рис. 17). При низкой концентрации субстрата, напротив, скорость реакции оказывается пропорциональной концентрации субстрата в каждый данный момент (реакция первого порядка).
Следует указать, что уравнение Михаэлиса–Ментен в его классическом виде не учитывает влияние на скорость ферментативного процесса продуктов реакции, например в реакции
![]()
и носит несколько ограниченный характер. Поэтому были предприняты попытки усовершенствовать его. Так, было предложено уравнение Бриггса-Холдейна:
![]()
где Кm представляет собой константу Михаэлиса, являющуюся экспериментально определяемой величиной. Она может быть представлена следующим уравнением:
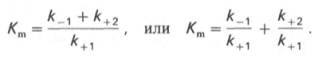
В числителе представлены константы скоростей распада комплекса ES в двух направлениях (в сторону исходных Е и S и в сторону конечных продуктов реакции Е и Р). Отношение k–1/ k+1представляет собой константу диссоциации фермент-субстратного комплекса KS, тогда:
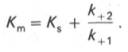
Отсюда вытекает важное следствие: константа Михаэлиса всегда больше константы диссоциации фермент-субстратного комплекса KS на величину
k+2/k+1.
Для определения численного значения Кm обычно находят ту концентрацию субстрата, при которой скорость ферментативной реакции v составляет половину от максимальной Vmax, т.е. если v = 1/2 Vmaх. Подставляя значение v в уравнение Бриггса–Холдейна, получаем:
![]()
разделив обе части уравнения на Vmах, получим
![]()
Таким образом, константа Михаэлиса численно равна концентрации субстрата (моль/л), при которой скорость данной ферментативной реакции составляет половину от максимальной.
Определение величины Кm имеет важное значение при выяснении механизма действия эффекторов на активность ферментов и т.д. Константу Михаэлиса можно вычислить по графику (рис.18). Отрезок на абсциссе, соответствующий скорости, равной половине максимальной, будет представлять собой Кm.
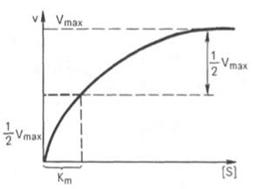
Рисунок 18 - Кривая уравнения Михаэлиса-Ментен: гиперболическая зависимость начальных скоростей катализируемой ферментом реакции от концентрации субстрата
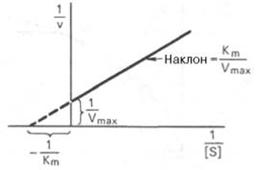
Рисунок 19 - График Лайнуивера-Бэрка
Пользоваться графиком, построенным в прямых координатах зависимости начальной скорости реакции v0 от начальной концентрации субстрата , неудобно, поскольку максимальная скорость Vmax в данном случае определяется недостаточно точно.
Для более удобного графического представления экспериментальных данных Г. Лайнуивер и Д. Бэрк преобразовали уравнение Бриггса–Холдейна и после преобразования получаем уравнение:
![]()
которое получило название уравнения Лайнуивера–Бэрка. Если теперь в соответствии с этим уравнением построить график в координатах 1/v (y) от l/ (x), то получим прямую линию (рис. 19), тангенс угла наклона который будет равен величине Km/Vmax; отрезок, отсекаемый прямой от оси ординат, представляет собой l/Vmax(обратная величина максимальной скорости). Если продолжить прямую линию за ось ординат, тогда на абсциссе отсекается отрезок, соответствующий обратной величине константы Михаэлиса – 1/Кm (см. рис. 4.14). Таким образом, величину Кm можно вычислить из данных наклона прямой и длины отрезка, отсекаемого от оси ординат, или из длины отрезка, отсекаемого от оси абсцисс в области отрицательных значений.
Поможем написать любую работу на аналогичную тему

