Описание термодинамических свойств ионов в растворах через активность и коэффициенты активности осуществляется в рамках теории Дебая-Хюккеля. В самом простейшем варианте теории будем считать все ионы точечными.
Вычислим электростатический потенциал отдельного иона в зависимости от расстояния от его центра. Для нахождения усредненного потенциала необходимо решить сферически симметричное уравнение Пуассона:
(9.4)
где 
-оператор Лапласа; 
- электростатический потенциал; 
- плонтость зарядов на расстоянии r от центрального иона. На расстоянии r от рассматриваемого иона концентрации положительных 
и отрицательных 
ионов изменяются в соответствии с законом Больцмана:
, 
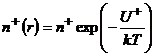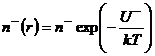(9.5)
где
, 
(9.6)
Z – абсолютное значение заряда иона в единицах заряда электрона; n+ и n- - средние концентрации анионов и катионов. Если в растворе присутствуют ионы с разными зарядами, то для получаем
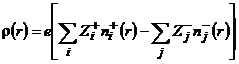(9.7)
Используя уравнения (9.5) и (9.6), получаем
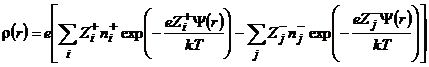(9.8)
Разлагая экспоненты в выражении (9.8) в ряд и ограничиваясь в каждом разложении двумя слагаемыми, а также учитывая электронейтральность раствора
(9.9)
получаем
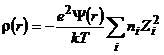(9.10)
где суммирование распространено на все катионы и анионы, присутствующие в растворе. Подставляя (9.10) в (9.4), находим
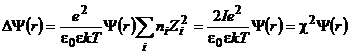(9.11)
Величина I называется ионной силой раствора:
(9.12)
Поможем написать любую работу на аналогичную тему