Уравнение Томсона

Обозначим через r радиус сферической поверхности раздела фаз (радиус капли), через Р0 – давление насыщеного пара над плоской (r = ¥), а через Р – над выпуклой поверхностью. Перенесем некоторое количество жидкости dm с плоской поверхности жидкости в каплю радиуса r путем обратимого изотермического испарения при давлении Р0, обратимого сжатия пара от Р0 до Р и последующей обратимой изотермической конденсации при Р. Поскольку работа испарения и конденсации равны и противоположны по знаку, то общая работа переноса dW, совершаемая над системой, оказывается работой сжатия пара:

,                                                                                                    (12.15)

где М – молярная масса вещества.

С другой стороны, в результате переноса dm вещества увеличивается масса капли за счет увеличения ее радиуса на dr и поверхность на dS, что требует затраты энергии на работу против сил поверхностного натяжения (работу увеличения поверхности).

В обоих случаях осуществляется перенос количества dm, поэтому работы dW1 и dW2 равны по абсолютной величине и противоположны по знаку:

.                                                                                               (12.16)

Так как m капли с радиусом r равна m = 4/3pr3r, где r - плотность жидкости - то dm = 4prr2dr. Поверхность капли S = 4pr2, поэтому dS = 8prdr. Подставим эти значения dm и dS в уравнение (12.16) и решим его относительно r. Получим:

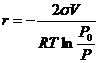                                                                                    (12.17)

(V – молярный объем жидкости ), что являет собой уравнение Томсона для выпуклой поверхности.

Для вогнутой поверхности кривизна отрицательна. Поэтому:

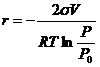.                                                                                                              (12.18)

Уравнение Томсона (Кельвина) и уравнение Лапласа являются основными уравнениями физической химии поверхностных явлений.

Следствия из полученных уравнений.

Давление пара (насыщенного) жидкости Р0 над плоской поверхностью (поверхность с r = ¥) меньше, чем давление пара над каплей радиуса r (Р0 < Р), но больше, чем давление пара Р над вогнутой поверхностью ( r < 0, Р0 > Р).

Чем меньше размер капли, тем больше равновесное давление ее насыщенного пара, и, следовательно, тем выше значение химического потенциала жидкости, т.е. тем не менее устойчиво ее состояние. Поэтому мелкие капли, обладая большим давлением пара, испаряются быстрее. Испарившееся вещество может конденсироваться на поверхности более крупных частиц и на плоской поверхности. Такой процесс роста крупных частиц за счет исчезновения (испарения) мелких носит название изотермической перегонки (переконденсации). Таким образом, всякая полидисперсная система термодинамически неравновесна, а поэтому неустойчива.

Равновесие твердых частиц по отношению к жидкому раствору можно выразить уравнением, сходным с уравнением Томсона. В растворе мерой интенсивности перехода вещества в другую фазу является концентрация насыщенного раствора, и тогда применительно к дисперсной системе твердая фаза – раствор можно записать:

,                                                                                                             (12.19)

где С0 – концентрация насыщенного раствора, С – концентрация вещества в растворе, равновесном с кристалликами размером r. Поэтому при растворении высокодисперсных веществ можно получить концентрацию раствора выше обычной растворимости.

Термодинамическая неравновесность таких систем обуславливает перекристаллизацию вещества – рост крупных кристаллов в пересыщенном растворе за счет растворения мелких. Например, для BaSO4 найдено, что растворимость частиц с размером r = 2 мкм равна 15,3 mмоль/л, а растворимость частиц с размером r = 0,3 мкм равна 18,2 mмоль/л. При подстановке этих данных в уравнение (12.19) найдем для величины tт-ж = 1250×10-3Дж/m2.

Повышение давления насыщенного пара над высокодисперсными частицами по сравнению с частицами крупных размеров обуславливает и некоторое понижение температуры их плавления. Например, уменьшение размера частиц салола до 8 мкм понижает его температуру плавления с 42 °С до 38 °С.