Задачи линейного программирования в производственном менеджменте

Составление линейных математических моделей

Задача линейного программирования является достаточно распространенной задачей принятия оптимальных решений в производственном менеджменте. Общая задача линейного программирования (ОЗЛП) математически может быть сформулирована следующим образом:

Найти значения переменных X1, X2, ..., Xn, максимизирующих (минимизирующих) линейную форму

F ()= c1 * X1 + c2 * X2 + ... + cn * Xn                            (1)

при условиях

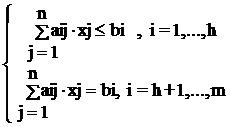,                         (2-3)

xj  0,  j = 1,...,p , (p n) .                                  (4)

Соотношения (2-3) называются функциональными ограничениями, а (4) – прямыми.

Пример 1. Металлургическому заводу требуется уголь с содержанием фосфора не более 0.03% и с долей зольных примесей не более 3.25%. Завод закупает три сорта угля А, В, С с известным содержанием примесей. В какой пропорции нужно смешивать исходные продукты А, В, С, чтобы смесь удовлетворяла ограничениям на содержание примесей и имела минимальную цену?

Содержание примесей и цена исходных продуктов приведены в табл. 1.

Таблица 1

Сорт	Содержание (%)		Цена
угля	фосфора Внимание! Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы. Расчет стоимостиГарантииОтзывы	золы	1 т, руб.
А В С	0.06 0.04 0.02	2.0 4.0 3.0	30 30 45

Построим математическую модель.

Обозначим:

Х1 – количество угля сорта А в тонне смеси;

Х2 – количество угля сорта В в тонне смеси, (переменные);

Х3 – количество угля сорта С в тонне смеси.

F() = 30×X1 + 30×X2  + 45×X3  -  стоимость 1 т. смеси (целевая функция),

0.06×Х1 + 0.04×Х2 + 0.02×Х3  0.03 (%) - ограничение на содержание фосфора в смеси,

2×Х1 + 4×Х2+ 3×Х3   3.25 (%) - ограничение на содержание зольных примесей,

Х1+ Х2 + Х3 = 1 (т.) - ограничение на состав 1 т. смеси.

Окончательно, математическая модель имеет вид.

Определить количество угля сортов А, В, С (Х1, Х2, Х3) в тонне смеси, при которых достигается

F() = 30×X1 + 30×X2  + 45×X3

при ограничениях

0.06×Х1 + 0.04×Х2 + 0.02×Х3  0.03

2×Х1 + 4×Х2 + 3×Х3   3.25

Х1 + Х2 + Х3 = 1

Х1,X2,X3  0.

Пример 2. Бройлерное хозяйство птицеводческой фермы насчитывает 20 000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Недельный расход корма в среднем (за 8 недель) составляет 500г = 0.5 кг.

Для того, чтобы цыплята достигли к 8-й неделе необходимого веса, кормовой рацион должен удовлетворять определённым требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов, или ингредиентов.

В табл. 2 приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента. Смесь должна содержать:

¨ не менее 0.8% кальция;

¨   не менее 22% белка (от общего веса смеси);

¨   не более 5% клетчатки.

Требуется определить количество (в кг) каждого из трёх ингредиентов, образующих смесь минимальной стоимости, при соблюдении требований к общему расходу кормовой смеси и её питательности.

Таблица 2

Ингредиент	Содержание питательных веществ (кг/ингредиента)			Стоимость (руб./кг)
	Кальций	Белок	Клетчатка
Известняк Зерно Соевые бобы	0.38 0.001 0.002	- 0.09 0.50	- 0.02 0.08	0.04 0.15 0.40

Математическая формулировка задачи.

Введём следующие обозначения:

Х1 - содержание известняка в смеси (кг);

Х2 - содержание зерна в смеси (кг);

Х3 - содержание соевых бобов в смеси (кг);

Общий вес смеси, еженедельно расходуемый на кормление цыплят:

20 000 * 0.5 = 10 000 кг.

Ограничения, связанные с содержанием кальция, белка и клетчатки в кормовом рационе, имеют вид:

0.38×Х1 + 0.001×Х2 + 0.002×Х3  0.008 * 10 000,

0.09×Х2 +  0.50×Х3   0.22 × 10 000,

0.02×Х2 +  0.08×Х3   0.05 × 10 000.

Окончательный вид математической формулировки задачи:

F() = 0.04×X1 + 0.15×X2  + 0.40×X3

при ограничениях

Х1 + Х2 + Х3 = 10 000

0.38×Х1 + 0.001×Х2 + 0.002×Х3  80

0.09×Х2 +  0.50×Х3   2200

0.02×Х2 +  0.08×Х3   500

Хj  0, j = 1, 2, 3.

Пример 3. В отделе технического контроля (ОТК) некоторой фирмы работают контролеры разрядов 1 и 2. Норма выработки ОТК за 8-часовой рабочий день составляет не менее 1800 изделий. Контролер разряда 1 проверяет 25 изделий в час, причем не ошибается в 98% случаев. Контролер разряда 2 проверяет 15 изделий в час; его точность составляет 95%.

Заработная плата контролера разряда 1 равна 4 руб. в час, контролер разряда 2 получает 3 руб. в час. При каждой ошибке контролера фирма несет убыток в размере 2 рубля. Фирма может использовать 8 контролеров разряда 1 и 10 контролеров разряда 2. Руководство фирмы хочет определить оптимальный состав ОТК, при котором общие затраты на контроль будут минимальными.

Математическая формулировка задачи.

Пусть X1 и X2 обозначают количество контролеров разрядов 1 и 2 соответственно. Число контролеров каждого разряда ограничено, т.е. имеются следующие ограничения:

X1 £ 8 (разряд 1)

X2 £ 10     (разряд 2)

Ежедневно необходимо проверять не менее 1800 изделий. Поэтому выполняется неравенство

8×25×X1 +  8×15×X2 = 200×X1 + 120×X2 ³ 1800,

или 5×X1 + 3×X2 ³ 45.

При построении целевой функции следует иметь в виду, что расходы фирмы, связанные с контролем, включают две составляющие:

1) зарплату контролеров.

2) убытки, вызванные ошибками контролеров.

Расходы на одного контролера разряда 1 в час составляют

4 руб. + 2×25×0,02 руб. = 5 руб.

Расходы на одного контролера разряда 2 в час составляют

3 руб. + 2×15×0,05 руб. = 4 руб.50 коп.

Следовательно, минимизируемая целевая функция, выражающая ежедневные расходы на контроль, имеет вид

8×(5×X1 + 4,5×X2) = 40×X1 + 36×X2.

Теперь можно сформулировать следующую задачу ЛП

F() = 40×X1 + 36×X2 

при ограничениях

X1 £ 8

X2 £ 10

5×X1 + 3×X2 ³ 45

X1,Х2  ³ 0 .

Пример 4. Промышленная фирма производит изделие, представляющее собой сборку из трех различных узлов. Эти узлы изготовляются на двух заводах. Из-за различий в составе технологического оборудования производительность заводов по выпуску каждого из трех видов узлов неодинакова. В приводимой ниже таблице содержатся исходные данные, характеризующие как производительность заводов по выпуску каждого из узлов, так и максимальный суммарный ресурс времени, которым располагает каждый из заводов для производства этих узлов.

Таблица 3

Завод	Максимальный недельный	Производительность, (узел/час)
	фонд времени, час	Узел 1	Узел 2	Узел 3
1	100	8	5	10
2	80	6	12	4

Идеальной является такая ситуация, когда производственные мощности обоих заводов используются таким образом, что в итоге обеспечивается выпуск одинакового количества каждого из видов узлов. Однако этого трудно добиться из-за различий в производительности заводов. Более реальная цель состоит, по-видимому, в том, чтобы максимизировать выпуск изделий, что, по существу, эквивалентно минимизации дисбаланса, возникающего вследствие некомплектности поставки по одному или двум видам узлов.

Требуется определить еженедельные затраты времени ( в часах) на производство каждого из трех видов узлов на каждом заводе, обеспечивающие максимальный выпуск изделий.

Математическая формулировка задачи.

Возможный объем производства каждого из трех видов узлов зависит от того, какой фонд времени выделяет каждый завод для их изготовления. Это послужит для нас исходным моментом при идентификации переменных.

Пусть xij – недельный фонд времени (в часах), выделяемый на заводе i для производства узлов вида j. Тогда объемы производства каждого из трех комплектующих узлов равны:

узел 1: 8 * x11 + 6 * x21,

узел 2: 5 * x21 + 12 * x22,

узел 3: 10 * x13 + 4 * x23.

Так как в конечной сборке каждый из комплектующих узлов представлен в одном экземпляре, количество конечных изделий должно быть равно количеству комплектующих узлов, объем производства которых минимален. Если, например, объем производства двух заводов составляет 100, 112 и 108 соответствующих узлов, то количество конечных изделий будет равно min {100,112,108}= 100. Поэтому количество конечных изделий можно выразить через число комплектующих узлов следующим образом:

min {(8 * x11 + 6 * x21), (5 * x12 + 12 * x22), (10 * x13 + 4 * x23)}.

Условия рассматриваемой задачи устанавливают ограничения только на фонд времени, которым располагает каждый завод. Таким образом, математическую модель  можно представить в следующем виде:

F() =  min{(8×x11+ 6×x21), (5×x12 + 12×x22), (10×x13 + 4×x23)}

при ограничениях

x11 + x12 + x13 £ 100 (завод 1);

x21 + x22 + x23 £ 80 (завод 2);

xij³ 0, i=1, 2; j=1, 2, 3.

Данная модель не является линейной, но ее можно привести к линейной форме с помощью простого преобразования. Пусть у – количество изделий

y = min { 8×x11 + 6×x21, 5×x12 + 12×x22, 10×x13 + 4×x23}.

Этому выражению с математической точки зрения эквивалентна следующая формулировка:

у

при ограничениях

8×x11 + 6×x21 ³ у

5×x12 + 12×x22 ³ у

10×x13 + 4×x23 ³ у

у ³ 0.

Можно убедиться в том, что максимизация у будет приводить к равенству этой переменной наименьшей из левых частей трех введенных ограничений, а это как раз и требуется.

Таким образом, окончательно математическую модель можно записать в виде

у

при ограничениях

8×x11 + 6×x21 – у ³ 0

5×x12 + 12×x22 – у ³ 0

10×x13 + 4×x23 – у ³ 0

x11 + x12 + x13 £ 100

x21 + x22 + x23 £ 80

xij ³ 0, i = 1, 2; j = 1, 2, 3, у ³ 0.

Пример 5. Фирма выпускает три вида продукции (изделий). В процессе производства используются три технологические операции. На рис. 1 показана технологическая схема производства изделий видов 1, 2 и 3. При изготовлении изделия 2 технологическая операция 2 не выполняется, а при производстве изделия 3 используются только технологические операции 1 и 2. В прямоугольниках на рис. 1 указана длительность технологических операций при изготовлении изделия каждого вида.

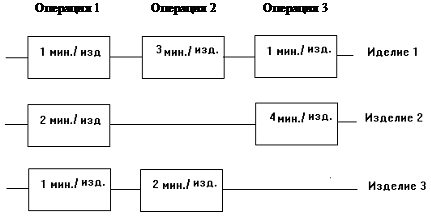
Рис. 1. Технологическая схема производства изделий

Так как эти технологические операции используются фирмой и для других производственных целей, фонд рабочего времени, в течение которого операции 1, 2 и 3 могут быть применены для производства рассматриваемых изделий, ограничен следующими предельными значениями (в сутки):

для первой операции - 430 мин,

для второй операции - 460 мин,

для третьей операции - 420 мин.

Изучение рынка сбыта показало, что ожидаемая прибыль от продажи одного изделия видов 1, 2 и 3 составляет 3,2 и 5 руб. соответственно.

Каков наиболее выгодный суточный объем производства каждого вида изделия?

Как уже было показано, построение математической модели следует начинать с идентификации управляемых переменных (искомых величин). После этого определяются целевая функция и ограничения через соответствующие переменные.

Пусть

X1 - количество производимых изделий вида 1,

X2 - количество производимых изделий вида 2,

X3 - количество производимых изделий вида 3.

При использовании этих обозначений математическая формулировка задачи принимает вид

F()= 3×X1 + 2×X2 + 5×X3  (целевая функция) (величина прибыли за сутки)

при ограничениях

для операции 1: 1×X1 + 2×X2 + 1×X3 £ 430 (предельное время

для операции 2: 3×X1 + 0×X2 + 2×X3 £ 460 использования операций

для операции 3: 1×X1 + 4×X2 + 0×X3 £ 420 в течение суток)

X1, X2, X3 ³ 0.

Геометрическая интерпретация задачи производственного планирования

Задачи производственного менеджмента  во  многих   случаях оказываются ассоциированными с задачами  распределительного  типа, т.е.  с  задачами,  в которых требуется распределить ограниченные ресурсы по нескольким видам производственной деятельности.

Рассмотрим следующую ситуацию, получившую название задачи производственного планирования. Пусть из технологических соображений известен перечень продуктов, которые предприятие может производить без дополнительных капиталовложений. Кроме того, известны вид и количество ресурсов отпущенных  предприятию  для  производственного  потребления   и структура  материальных затрат и доходов.  В этих условиях перед предприятием   стоит задача выбора плана производства, обеспечивающего получение максимальной прибыли.

Перейдем к построению математической  модели  рассмотренной ситуации.  Будем  считать, что  предприятие  может  производить n различных  продуктов  (j = 1, ..., n). Количество   j-го   продукта выпускаемого  по плану,  обозначим через xj.  В этом случае план производства может быть описан с помощью  вектора  = (X1, X2, ..., Xn). Предположим,  что  предприятие  располагает  для организации производственного процесса m видами различных ресурсов (i = 1, ..., m).  Количество  ресурса  i-го вида,  отпущенное предприятию для потребления обозначим через bi.  Количество ресурса  i-го  вида, расходуемое  предприятием на производство единицы j-го продукта, обозначим  через  aij,  а  прибыль,  от   производства   единицы продукции j-го вида через cj.

Тогда, в принятых нами обозначениях,  задача  выбора  плана производства,  обеспечивающего  получение  максимальной  прибыли может быть сформулирована как математическая задача  в следующем виде:

 Найти вектор-план    =(X1,X2,...,Xn),    удовлетворяющий системе ограничений

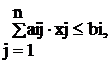 i=1,...,m,

Xj0 ,

и доставляющий целевой функции задачи

F() = 

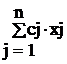
максимальное значение.

Пример 1.  Предприятие  производит  два  вида  продукции  А1,  А2 , используя  сырье  трех  типов:  S1, S2, S3.  Нормы  расхода  сырья каждого типа на единицу продукции,  их  наличие  в  распоряжении предприятия,  а  также  прибыль  от реализации единицы продукции приведены в таблице 1. Требуется составить   такой  план  выпуска  продукции,  при котором  прибыль   предприятия   от   ее   реализации   является максимальной.

Таблица 1

Вид	Норма расхода сырья  на  единицу продукции		Наличие
сырья	А1	А2	сырья
S1	1	1	5
S2	2	1	9
S3	1	2	7
Прибыль от единицы продукции	3	4

Математическая модель данной задачи может  быть  записана следующим образом. Определить объемы производства продукции вида А1 и А2, при которых достигается максимум целевой функции

F()= 3×X1 + 4×X2

при ограничениях

X1 + X2   5

2×X1 + X2   9

X1 + 2×X2  7

X1,X2  0   ,

где X1 и X2 - количество единиц продукции вида А1 и А2.

С формальных   позиций   данная  модель  является  линейной потому, что все входящие в нее функции линейные. Так как модель  содержит  только  две  переменные,  задачу  можно решить графически.

Первый шаг,    при   использовании   графического   метода, заключается в геометрическом представлении  допустимых  решений, т.е.  построении области, в которой одновременно выполняются все ограничения  модели.  Искомая  область  (пространство)  решений показана на рис. 1.

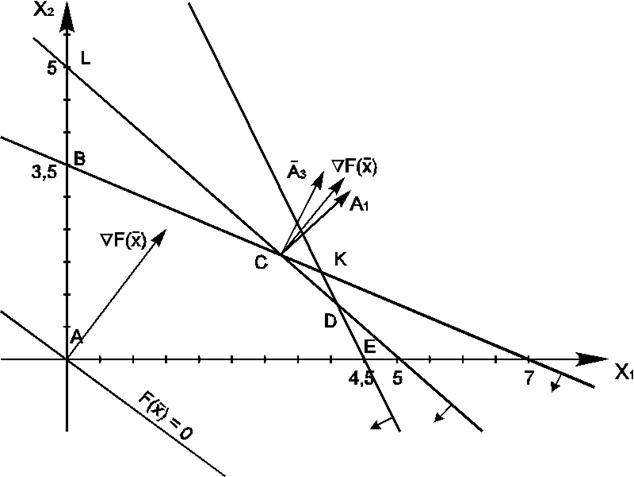Рис. 1. Геометрическая интерпретация задачи производственного планирования

Пространство решений  содержит  бесконечное  число  точек. Известно,  что  направление  возрастания  целевой функции модели определяется вектором-градиентом,  т.е.  вектором с координатами (3;4) – . На рис.1  это направление показано стрелкой. Чтобы найти оптимальное решение,  следует перемещать прямую  характеризующую прибыль   (линию   уровня   целевой   функции)   в   направлении вектора-градиента до тех пор,  пока она не сместится  в  область недопустимых  решений.  Из  рис.1 видно, что оптимальному решению соответствует точка С с координатами (3;2).  Полученное  решение означает,   что  объем  производства  продукции  А1  равен  трем единицам,  а  продукции  А2  равен  двум  единицам.  Прибыль  от реализации составит 17 денежных единиц. Заметим, что оптимальному решению   всегда  может  быть поставлена в  соответствие  одна  из  допустимых  угловых  точек  пространства решений  (на  рис.1 это точки А,B,С,D,Е).  Какая из этих точек окажется оптимальной, зависит от наклона линии уровня целевой функции, т.е. от коэффициентов целевой функции.

Основы анализа на чувствительность (анализ модели после нахождения оптимального решения)

После того как оптимальное решение получено  выявляется его чувствительность к  определенным  изменениям исходной модели.  В нашей задаче, например, могут представить интерес вопросы о том, как повлияет  на  оптимальное  решение изменение запасов сырья и изменение прибыли от единицы продукции.

В связи с этим представляется логичным выяснить:

1. На сколько можно увеличить запас некоторого  вида  сырья для улучшения полученного оптимального значения целевой функции?

2. На сколько можно снизить запас некоторого вида сырья при сохранении полученного оптимального значения целевой функции?

3. Увеличение объемов какого вида сырья наиболее выгодно?

4. Каков  диапазон  изменения  того  или иного коэффициента целевой функции,   при   котором   не    происходит    изменения оптимального решения?

Прежде чем ответить на первые два  вопроса,  классифицируем ограничения на  активные  и неактивные.  Прямая,  представляющая активное ограничение,  должна проходить через оптимальную точку.  В противном случае соответствующее ограничение будет неактивным.  На рис.1 активными ограничениями являются (1) и  (3),  т.е.  те, которые лимитируют запасы сырья S1 и S3.

Если некоторое  ограничение  является   активным,   логично отнести соответствующее  сырье  к разряду дефицитных,  т.к.  оно расходуется полностью. Сырье, с которым ассоциируется неактивное ограничение, следует отнести к разряду недефицитных, так как оно имеется в некотором избытке.  В нашей задаче используемое  сырье S1 и S3 является дефицитным.

Рассмотрим вначале  сырье  S1  (ограничение  1).  Из  рис.1 видно, что   при  увеличении  запаса  этого  вида  сырья  прямая (1) (отрезок СД)  перемещается  вверх  параллельно  самой  себе, постепенно стягивая   в   точку   треугольник  СКД.  В  точке  К становятся активными ограничения (2) и (3). Оптимальному решению при этом  будет  соответствовать точка К,  в которой ограничение (1) становится неактивным.  Поэтому дальнейший рост запаса сырья S1 не следует увеличивать сверх того предела,  когда ограничение становится неактивным (избыточным).

Этот предельный   уровень  определяется  путем  подстановки координат точки К(11/3;5/3) в левую  часть  ограничения  (1).  В результате получим

1×11/3 + 1×5/3 = 16/3,

F(K) = 3×11/3 + 4×5/3 = 53/3.

Аналогично рассматривается    вопрос   о   целесообразности увеличения запаса дефицитного сырья S3.  Из рис.1 видно, что при увеличении этого вида сырья прямая (3) (отрезок BС) перемещается вверх параллельно  самой  себе.  В  точке  L   ограничение   (3) становится неактивным,   поэтому   объем  сырья  S3  не  следует увеличивать сверх  этого  предела.   Этот   предельный   уровень определяется путем  подстановки  координат  точки L(0;5) в левую часть ограничения (3). В результате получим

1×0 + 2×5 = 10,

F(L) = 3×0 +4×5 = 20.

Рассмотрим теперь вопрос об уменьшении запаса недефицитного сырья S2  (ограничение  2).  Из  рис.1  видно,  что  не  изменяя оптимального решения прямую (2)  (отрезок  КЕ)  можно  перемещать параллельно самой  себе  до  пересечения с точкой С.  Уменьшение запаса сырья S2 до величины 8 (2×3 + 1×2 = 8) никак  не повлияет на оптимальность полученного ранее решения.

Результаты проведенного анализа помещены в таблице 2.

Таблица 2

Сырье	Тип сырья	Максимальное изменение запаса	Максимальное изменение прибыли
S1	дефицитное	16/3 - 5 = 1/3	53/3 - 51/3 = 2/3
S2	недефицитное	9 - 8 = 1	17 - 17 = 0
S3	дефицитное	10 - 7 = 3	20 - 17 = 3

Для ответа  на третий вопрос введем характеристики ценности каждой дополнительной   единицы   сырья.   Обозначим    ценность дополнительной единицы i-го вида сырья через Yi, где     

Yi ={ максимальное приращение F() /  максимальное  изменение запаса сырья Si}.

Тогда Y1 = 2, Y2 = 0, Y3 = 1.

Полученные результаты свидетельствуют о том, что дополнительные вложения в первую очередь следует направлять на закупку сырья  S1 и лишь затем - на закупку сырья S3.

При выяснении  вопроса  относительно  величины   диапазона изменения того или иного коэффициента целевой функции, в котором не происходит изменения оптимального решения опять  обратимся  к рис.1. Из  него видно,  что при небольшом изменении коэффициентов целевой функции с1 и с2 прямая F() =17 вращается  вокруг  точки  С.  Таким образом,  точка  С будет оставаться оптимальной до тех пор пока прямая F() не выйдет за  пределы,  определяемые  первым  и третьим ограничениями {пока вектор  будет находиться между нормалями к первому и третьему ограничениям}.

Определим сначала диапазон изменения  коэффициента  с1  при фиксированном коэффициенте  с2  (с2 = 4).  Тангенсы углов наклона для векторов , , соответственно равны : tg() = c2/c1 , tg(1) = 1, tg (3) = 2.

Поэтому диапазон изменения коэффициента с1 в целевой функции определится из соотношения   1£ c2/c1 £ 2 , т.е.   2 £ c1 £ 4.

Диапазон изменения  коэффициента c2  при  фиксированном c1 (c1 = 3) определяется аналогично, т. е.  3 £  c2  £  6.

Симплекс-метод решения задачи производственного планирования

Все точные методы решения общей задачи линейного программирования (ОЗЛП) косвенные , т.е. не непосредственно решаем ОЗЛП, а решаем некоторую другую задачу и на основе ее делаем вывод о решении ОЗЛП. Такой косвенной задачей в ЛП является каноническая задача линейного программирования (КЗЛП).

Канонической задачей линейного программирования будем называть следующую задачу:

F() = () max (min)                                        (1)

A =                                                        (2)

0                                                         (3)

rang (A) = m < n,                                               (4)

где  = (c1, c2, ..., cn)T,  = (X1,X2 , ..., Xn)T,

A = (aij) m, n = (,, ..., ),  = (b1, b2, ..., bm)T,   0.

Если целевая функция имеет конечный экстремум, то по крайней мере одно оптимальное решение является базисным (вершиной допустимого множества). Это означает, что при поиске оптимального решения в допустимой области можно ограничиться базисными допустимыми решениями. 

В вычислительной схеме симплекс-метода реализуется вычислительный процесс, при котором, начиная с некоторой допустимой вершины (обычно начала координат), осуществляются последовательные переходы от одной допустимой вершины к другой, до тех пор, пока не будет найдена точка, соответствующая оптимальному плану.

Канонический вид, рассмотренной в параграфе 1.2 , задачи производственного планирования будет следующим:

F() = 3×X1 + 4×X2  + 0×X3 + 0×X4 + 0×X5  max

при ограничениях

X1 +   X2 + X3  = 5

2×X1 + X2  + X4 = 9

X1 + 2×X2  +X5 = 7

Xj  0, j = 1, ..., 5.

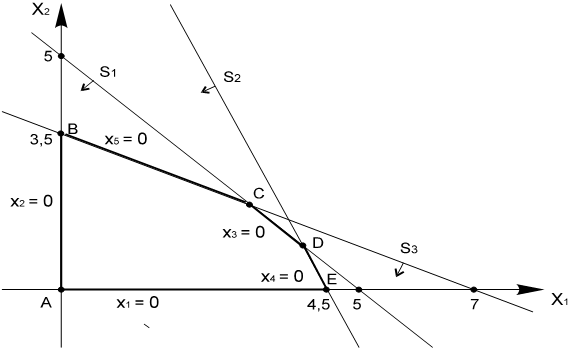
Рис. 1 Геометрическая интерпретация задачи производственного планирования

Каждую точку пространства решений можно определить с помощью переменных X1, X2, X3, X4, X5. Увеличение переменных X3, X4, X5 будет соответствовать смещению допустимых точек с границ пространства решений в его внутреннюю область. Нас интересует прежде всего алгебраическое представление вершин допустимого множества. Анализируя рисунок можно записать:

Вершина	нулевые переменные (свободные)	ненулевые переменные (базисные)
A B C Д E	x1, x2 x1, x5 x3, x5 x3, x4 x2, x4	x3, x4, x5 x2, x3, x4 x1, x2, x4 x1, x2, x5 x1, x3, x5

Смежные вершины (крайние точки) отличаются только одной переменной в каждой группе свободных и базисных переменных. Все допустимые вершины определяются как  все неотрицательные базисные решения системы линейных уравнений (2).

Расширенную матрицу системы линейных уравнений, которая определяет неотрицательное базисное решение исходной системы будем называть К-матрицей.

Пусть = (,, ..., ) - базисная подматрица , т.е. матрица составленная из столбцов (,, ..., ) матрицы , образующих на s-й итерации симплекс-метода единичную подматрицу.

Матрица K(S) может быть получена следующим образом:

.

Тогда        

.

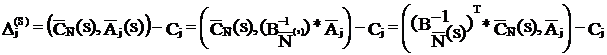В нашей задаче

,

, , .

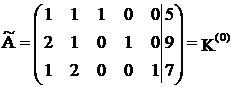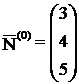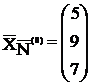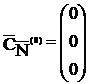K(0) определяет исходный опорный план.  Это вершина А  на рис. 1.  Приведем решение, рассмотренной выше, задачи в симплекс-таблице.

Таблица 1

номер итерации			3	4	0	0	0	=
0	3 4 5	0 0 0	1 2 1	1 1 2	1 0 0	0 1 0	0 0 1	5 9 7
			-3	-4	0	0	0	F(X) = 0
1	3 4 2	0 0 4	1/2 3/2 1/2	0 0 1	1 0 0	0 1 0	-1/2 -1/2 1/2	3/2 11/2 7/2
			-1	0	0	0	2	F(X) = =14
2	1 4 2	3 0 4	1 0 0	0 0 1	2 -3 -1	0 1 0	-1 1 1	3 1 2
			0	0	2	0	1	F(X) = =17

Из последней итерации симплексной таблицы можно получить информацию относительно оптимального плана, статуса сырья, ценности сырья, чувствительности базиса к изменению запасов сырья и  вариациям коэффициентов целевой функции.

а) оптимальное решение.

Используя данные симплекс-таблицы основные результаты можно представить в следующем виде:

= (3, 2, 0, 1, 0),

X1 = 3 - объем производства продукции вида А1,

X2 = 2 - объем производства продукции вида А2,

F()= 17 - прибыль от реализации продукции.

б) статус видов сырья.

Сырье S1 - дефицитное, так как значение остаточной переменной X3 равно нулю. Сырье S2 - недефицитное, так как значение остаточной переменной X4 равно единице. Положительное значение остаточной переменной указывает на неполное использование соответствующего вида сырья. Сырье S3 - дефицитное, так как значение остаточной переменной X5 равно нулю. Увеличение запасов сырья S1 и S3 позволит улучшить найденное решение.

в) ценность сырья.

Ценность различных видов сырья характеризуется величиной улучшения оптимального значения F(), приходящегося на единицу прироста соответствующего вида сырья:

, .

Как следует из теории линейного программирования ценность видов сырья можно определить по формуле:

,  , где

- номер единичного столбца с единицей на i-м месте в матрице ,

- коэффициент при переменной в целевой функции,

- симплексная разность при переменной в последней итерации.

В нашем примере:

Y1 = = 2 + 0 = 2

Y2 = = 0 + 0 = 0

Y3 =  = 1 + 0 = 1.

г) чувствительность базиса к изменению запасов сырья.

Предположим, что запас первого вида сырья изменился на  , т.е. теперь он составляет 5+ единиц. Введение  скажется только на правой части симплекс-таблицы. Все же изменения правой части можно непосредственно определить по данным симплекс-таблицы. А именно, коэффициенты при  в правых частях ограничений будут равны коэффициентам при первой остаточной переменной, т.е. при переменной X3. Так как изменение запаса сырья может повлиять на допустимость базисного решения, то величина  должна быть ограничена решением системы неравенств:

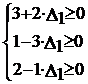
  -3/2  1/3 или () .

В данном диапазоне изменения запаса сырья S1 переменные X1, X4, X2 остаются базисными и определяют оптимальное базисное решение. В этом случае остаются неизменными виды производственной деятельности.

При исследовании чувствительности базиса к изменению запасов сырья S2  и S3 поступим аналогично. Соответственно получим:

,

,

, .

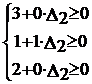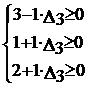
Так как изменение запасов сырья может повлиять только на допустимость решения, то интервалы изменения запасов сырья  в общем случае определятся из соотношений:

×,

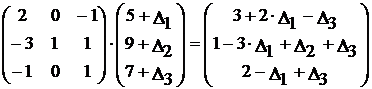Þ  .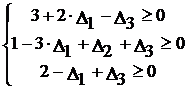

д) чувствительность оптимального плана к вариациям коэффициентов целевой функции.

Так как любые изменения коэффициентов целевой функции оказывают влияние на симплексные разности, то такие изменения могут сделать полученное решение неоптимальным. Предположим, что коэффициент  изменился на  , а коэффициент  остался без изменения, т.е.

F()=

Симплексные разности при базисных переменных X1, X4, X2 останутся равными нулю. Коэффициенты при  в симплексных разностях небазисных переменных X3 и X5 будут равны коэффициентам при этих переменных в уравнении соответствующем базисной переменной X1, так как именно при этой переменной изменился коэффициент. Таким образом получим

  , .

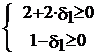
Аналогично для случая

F() =

получим

  , .

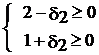
Любое изменение коэффициента целевой функции при небазисной переменной приводит лишь к тому, что в заключительной симплексной таблице изменяется только симплексная разность соответствующей этой переменной. В таком случае необходимо требовать , если изменился коэффициент при k-й переменной.

Изменение коэффициентов целевой функции оказывает влияние на оптимальность полученного ранее решения.  Поэтому допустимые интервалы изменения коэффициентов целевой функции в общем случае определятся из следующих соотношений:

.

  = .

,

,

,

,

,

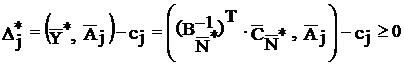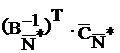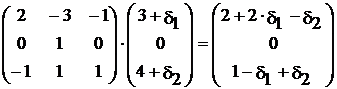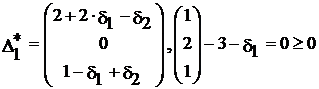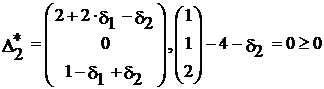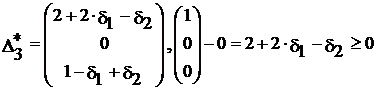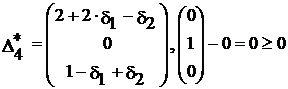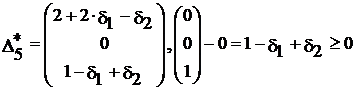Þ .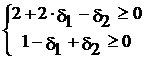

Альтернативные оптимальные решения

Когда гиперплоскость, представляющая целевую функцию, параллельна гиперплоскости, соответствующей связывающему ограничению ( которое в точке оптимума выполняется как точное равенство), целевая функция принимает одно и то же оптимальное значение в некоторой совокупности точек пространства решений. Такие решения называются альтернативными оптимальными решениями.

Приводимый ниже пример рассматриваемой ситуации показывает, что при этом обычно существует бесконечное множество альтернативных решений.

Пример:

F()= 2×x1 + 4×x2 max

при ограничениях

x1 + 2×x2 £ 5 (ресурс 1)

x1 + x2 £ 4 (ресурс 2)

x1 ³ 0, x2 ³ 0.

Рис.2 иллюстрирует условия данной задачи ЛП, особенность которой состоит в том, что прямая, представляющая целевую функцию, параллельна прямой, соответствующей одному из связывающих ограничений.

Рис. 2. Геометрическая интерпретация альтернативных базисных решений

Это обусловливает наличие альтернативных оптимальных решений. Любая точка отрезка ВС представляет собой альтернативный оптимум, причем в каждой из этих точек целевая функция имеет одно и то же оптимальное значение. Приведем решение задачи в симплекс-таблице.

Таблица 2

						=
3 4	0 0	1 1	2 1	1 0	0 1	5 4
		-2	-4	0	0	F(x) = 0
2 4	4 0	1/2 1/2	1 0	1/2 -1/2	0 1	5/2 3/2
		0	0	2	0	F(x) = 10
2 1	4 2	0 1	1 0	1 -1	-1 2	1 3
		0	0	2	0	F(x) = 10

Каким образом по результатам итерации можно узнать о наличии альтернативных решений?

Нулевое значение симплексной разности у небазисной переменной свидетельствует о том, что ее включение в базис не изменит значения целевой функции, но приведет к изменению других переменных.

Любое решение, соответствующее точке (,)  принадлежащей отрезку ВС, можно определить как положительно-взвешенное среднее двух полученных оптимальных базисных решений, соответствующих точкам В и С. Поэтому, используя координаты точек В и С

В: х1 = 0; х2 = 5/2;

С: х1 = 3; х2 = 1;

и полагая , можно выразить координаты любой точки отрезка ВС следующим образом:

,

.

Информация о наличии альтернативных оптимумов дает возможность выбора альтернативного варианта в наибольшей степени отвечающего сложившейся производственной ситуации.

Метод искусственного базиса

Часто, после приведения ОЗЛП к каноническому виду расширенная матрица системы линейных уравнений (СЛУ) не является К-матрицей (нет начального опорного плана), и, следовательно, решать такую КЗЛП симплекс-методом нельзя. Суть метода искусственного базиса состоит в следующем: строится такая вспомогательная КЗЛП (ВКЗЛП) с заранее известным опорным планом, по решению которой либо определяется начальный опорный план исходной задачи, либо устанавливается, что ее множество планов пусто.

Дано:

, i = 1, ..., m, rang (A) = m < n, bi  0, i = 1, ..., m.

Найти: К-матрицу (начальный опорный план).

Построим следующую ВКЗЛП:

,

, i = 1, ..., m, xj  0, j = 1, ..., n, yi  0, i = 1, ..., m, yi – искусственные переменные.

Очевидно, начальный опорный план ВКЗЛП имеет вид:

,

= (n+1, n+2, ..., n+m).

Применяя симплекс-метод, находят

 – решение ВКЗЛП.

Замечание: ВКЗЛП всегда разрешима, так как множество ее планов не пусто, а целевая функция ограничена.

Теорема: Если , то  – начальный опорный план исходной КЗЛП. Если , то множество планов исходной КЗЛП пусто и, следовательно, она неразрешима.

Пример: F(X) = 5×x1 +  3×x2 +  4×x3 - x4

x1 + 3×x2 + 2×x3 + 2×x4 = 3

2×x1 + 2×x2 + x3 + x4 = 3

.

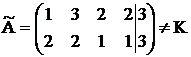x1 + 3×x2 + 2×x3 + 2×x4 + y1 = 3

x1 + 3×x2 + 2×x3 + 2×x4 + y2 = 3

xj0, j = 1, ..., 4, y1,20.

= (5,6),  = (3,3), = (-1,-1).

Таблица 1

								=
5 6	-1 -1	1 2	3 2	2 1	2 1	1 0	0 1	3 3
		-3	-5	-3	-3	0	0	F(x)=-6
2 6	0 -1	1/3 4/3	1 0	2/3 -1/3	2/3 -1/3		0 1	1 1
		-4/3	0	1/3	1/3		0	-1
2 1	0 0	0 1	1 0	3/4 -1/4	3/4 -1/4			3/4 3/4
		0	0	0	0			F(x)=0

Замечание:

По мере выхода искусственных переменных из базиса, вычисления в соответствующих клетках симплекс-таблицы не проводятся.

Получили оптимальный опорный план ВКЗЛП.

 (3/4,3/4,0,0,0,0), , (3/4,3/4,0,0).

Теперь решаем симплекс-методом исходную задачу:

F(X)= 5×x1 +  3×x2 +  4×x3 - x4

x2 + 3/4×x3 + 3/4×x4 = 3/4

x1 - 1/4×x3 - 1/4×x4 = 3/4

xj0, j = 1, ..., 4.

Таблица 2

						=
2 1	3 5	0 1	1 0	3/4 -1/4	3/4 -1/4	3/4 3/4
		0	0	-3	2	F(x) = 6
3 1	4 5	0 1	4/3 1/3	1 0	1 0	1 1
		0	4	0	5	F(x) = 9

(1, 0, 1, 0), = 9.

Анализ решаемых задач

Математическая модель является хорошим средством получения ответов на широкий круг самых разнообразных вопросов, возникающих при принятии оптимальных решений. Например, на этапе постановки задачи часто производится анализ с целью ответа на вопросы: “что будет, если...?“ и/или “что надо, чтобы...?”. Анализ с целью ответа на первый вопрос называется вариантным анализом; на второй - решениями по заказу. Для задач распределения ресурсов большой интерес представляет решение  задачи минимизации используемых ресурсов при заданном результате.

Рассмотрим следующую исходную задачу:

Первая постановка:

F()=  4X1 + 3X2  + 6X3 + 7X4   (прибыль)

при ограничениях на ресурсы

2X1 +   X2 +    X3 + X4    280           -     ( трудовые)

X1            +    X3 + X4    80              -      (сырье)

X1 + 2X2 +  X3             250            -     (финансы)

Xj  0,   j=1,...,4 .

Решив задачу получим:  = (0, 125, 0, 80) ,   где

X1 = 0 - объем производства продукции вида 1,

X2 = 125 - объем производства продукции вида 2,

X3  = 0 - объем производства продукции вида 3,

X4 = 80 - объем производства продукции вида 4.

F() = 935 - прибыль от реализации продукции.

Вторая постановка:

F()=  4X1 + 3X2  + 6X3 + 7X4   (прибыль)

при ограничениях на ресурсы

2X1 +   X2 +    X3 + X4    280           -     ( трудовые)

X1            +    X3 + X4   80               -    (сырье)

X1 + 2X2 +  X3            250              -   (финансы)

X1 10 ,       X2  100,              -        (дополнительные

X3   25 ,                                             ограничения на

X4    50                                             выпуск продукции)

Xj0,     j=1,...,4.

В результате  решения получим: = (10, 100, 25, 45) ,    F() = 805.

Третья постановка:

F() =  Y1 + Y2  + Y3       (минимизация используемого ресурса)

2X1 +   X2 +    X3 + X4  + Y1  = 280          -      ( трудовые)

X1            +    X3 + X4  + Y2 = 80              -         (сырье)

X1 + 2X2 +  X3          + Y3  = 250            -        (финансы)

X1 10 ,       X2  20               -      (задаваемый

X3   25 ,     X4   40.                        результат)

Y1 , Y2  ,   Y3 0           -    ( неиспользованный ресурс).

Решив задачу получим: = (10, 20, 25, 40) ,  = (175, 5, 175).

При решении по заказу пользователь задает значения тех величин, которые он хочет иметь в оптимальном решении. Такие задачи могут быть трех видов:

1) назначение величины целевой функции;

2) назначение величин искомых переменных;

3) назначение величин используемых ресурсов.

Следует иметь в виду, что во всех этих случаях возможно появление несовместного решения. Рассмотрим такую ситуацию на нашем примере.

Четвертая постановка:

F()=  4X1 + 3X2  + 6X3 + 7X4      (прибыль)

при ограничениях на ресурсы

2X1 +   X2 +    X3 + X4    280         -       ( трудовые)

X1            +    X3 +  X4   80             -      (сырье)

X1 + 2X2 +  X3            250           -      (финансы)

X1 100 ,       X2  100,                   -    (дополнительные

X3 =  30 ,     X4 = 70                ограничения на выпуск продукции)

Xj0,     j=1,...,4 .

Очевидно, что для выпуска такого количества продукции располагаемых ресурсов будет недостаточно. Найдем минимальные значения дополнительных необходимых ресурсов каждого вида позволяющих удовлетворить ограничениям задачи.

Пятая постановка:

F() = t1 + t2  + t3  (минимизация необходимого дополнительного ресурса)

2X1 +   X2 +    X3 + X4  - t1  = 280          -      ( трудовые)

X1             +    X3 + X4  - t2 = 80              -      (сырье)

X1 + 2X2 +  X3           - t3  = 250           -    (финансы)

X1 100 ,       X2  100,             -         (задаваемый результат)

X3 =  30 ,     X4 =  70.

t1 , t2  , t3 0      -         (дополнительный ресурс).

Решив задачу получим: = (100, 60, 30, 70) ,  = (80, 120, 0).