Специальные задачи линейного программирования в производственном менеджменте

Задачи дробно-линейного программирования

Общая задача дробно-линейного программирования состоит в определении экстремального значения функции

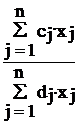= =                                (2.1)

при условиях

, i = 1, ..., m,                             (2.2)

xj  0,  j=1,...,n ,                                  (2.3)

где cj, dj, bi и aij - некоторые числа,  причем 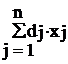 > 0 в области допустимых решений. Такое условие не нарушает общности задачи, поскольку в том случае когда эта величина отрицательна, знак минус можно отнести к числителю. Как и в случае основной задачи линейного программирования, экстремальное значение целевая функция (2.1) принимает в одной из вершин допустимого  многогранника (естественно, при условии, что эта задача имеет оптимальный план).

Рассмотрим несколько содержательных примеров на составление математической модели.

Пример 1. Для производства n видов изделий предприятие использует m типов взаимозаменяемого оборудования. Каждый из видов изделий необходимо изготовить в количестве bj единиц (j=1,..,n), причем каждый из типов оборудования может быть занят изготовлением этих изделий не больше чем ai часов (i=1,...,m). Время изготовления одного изделия j-го вида на i-м типе оборудования равно aij часам, а затраты, связанные с производством одного изделия на данном типе оборудования равны cij рублей. Определить сколько изделий каждого вида на каждом из типов оборудования следует произвести так, чтобы себестоимость одного изделия была минимальной.

Пусть Xij - количество изделий j-го вида, изготовляемых на оборудовании i-го типа. Тогда получим

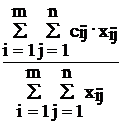
  (себестоимость одного изделия)

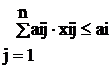 (i=1, ..., m) – (ограничения на время),

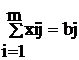 (j = 1, ..., n) – (ограничения на выпуск изделий),

Xij  0,  (i=1,...,m),  ( j=1,...,n)    - (условия неотрицательности).

Пример 2. Для выполнения n различных работ могут быть использованы рабочие m квалификационных групп. При выполнении j-й работы i-й группой рабочих выработка в единицу времени равна cij  (i=1,...,m), ( j=1,...,n) рублей. Общий фонд времени, в течение которого i-я группа рабочих может быть занята выполнением работ, не превышает bi единиц времени, а объем j-й работы равен aj рублей. Составить такой план выполнения работ, при котором производительность труда является максимальной.

Пусть Xij - время, выделяемое рабочими i-й квалификационной группы на j-ю работу. Тогда

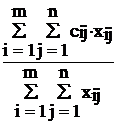
   – (производительность труда),

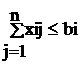     (i=1,...,m)  - (ограничения на время),

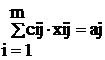     (j=1,...,n) – (ограничения на объем работы),

Xij  0, (i = 1, ..., m), (j = 1, ..., n) – (условия неотрицательности).

Сформулированная выше задача (2.1)-(2.3) может быть сведена к задаче линейного программирования. Для этого следует обозначить

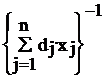                                                 (2.4)

и ввести новые переменные , (j = 1, ..., n).   (2.5)

Тогда исходную задачу  (2.1)-(2.3) можно записать в виде

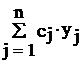                                               (2.6)

при условиях

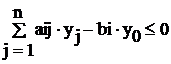,    (i=1,...,m),              (2.7)

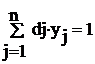                                                    (2.8)

0,  ( j=1,...,n), 0.

Задача (2.6) - (2.8) является задачей линейного программирования и , следовательно, ее решение можно найти известными методами. Зная оптимальный план этой задачи, на основе соотношений (2.5) получим оптимальный план исходной задачи  (2.1) - (2.3).

Пример 3 .

=  

2 * X1 + X2 + X3 + 3 * X4 £ 300

X1 + 2 * X3 +  X4 £ 70

X1 + 2 * X2 + X 3 £ 340

Xj  0, (j = 1, ..., 4).

Сведем данную задачу к задаче линейного программирования. Для этого обозначим  через  и введем новые переменные

  ,   (j=1,...,4).  В результате приходим к следующей задаче:

 8 * Y1 + 3Y2 + 2 * Y3 + Y4

2 * Y1 + Y2 + y3 + 3 * Y4 - 300 * Y0  £  0

Y1 + 2 * Y3 + Y4 - 70 * Y0 £ 0

Y1 + 2 * Y2 + y3 - 340 * Y0 £ 0

Y1 +   Y2 + Y3 +  Y4 = 1

Y0, Yj  0,  ( j=1,...,4).

Решив данную задачу получим:

 (Y0, Y1, Y2, Y3, Y4) = ( 1/70, 1, 0, 0, 0)

Используя соотношения , определяем оптимальный план исходной задачи

 (X1, X2, X3, X4) = (70, 0, 0, 0), F() = 8.

Задачи целочисленного программирования

Значительная часть задач производственного менеджмента, относящихся к задачам линейного программирования, требует целочисленного решения. К ним относятся задачи, у которых переменные величины означают количество единиц неделимой продукции.

Целочисленное программирование ориентировано на решение задач, в которых все или некоторые переменные должны принимать только целые значения. Задача называется полностью целочисленной, если условие целочисленности наложено на все ее переменные; когда это условие относится лишь к некоторым переменным, задача называется частично целочисленной.

Математическая модель линейной целочисленной задачи может быть записана следующим образом:

F() =                        (1)

, bi  0, i = 1, ..., m,                      (2)

xj  0, j = 1, ..., n, xj – целые.                                  (3)

Существует эвристический подход к решению задач целочисленного программирования (ЗЦП), основанный на решении ЗЦП как задачи ЛП. Использование процедур округления нецелочисленного оптимального решения задачи ЛП дает возможность получать приближенное оптимальное целочисленное решение. Например, если в оптимальном решении двумерной задачи ЛП значения переменных х1 и х2 оказались равными 3,5 и 4,4 соответственно, то в качестве кандидатов на роль приближенного целочисленного оптимального решения необходимо рассмотреть точки (3;4), (4;4), (4;5), (3;5) полученные в результате округления. Заметим однако, что истинное оптимальное целочисленное решение может не совпадать ни с одним из четырех, указанных выше.

ПРИМЕР

F() = x1 – 3×x2 + 3×х3

при ограничениях

2×x1 + x2 - х3 £ 4

4×x1 - 3×x2 £ 2

-3×x1 + 2×x2 + х3 £ 3

x1, х2, х3 ³ 0, целые.

Игнорируя условия целочисленности получим . Никакое округление компонент этого плана не дает допустимого решения, так как искомое целочисленное решение . Таким образом, для решения целочисленных задач необходимы специальные методы.

Точные методы решения задач целочисленного программирования можно классифицировать как методы отсечений и комбинаторные методы.

Название “методы отсечений” связано с тем обстоятельством, что вводимые дополнительные ограничения отсекают некоторые области многогранника допустимых решений, в которых отсутствуют точки с целочисленными координатами. Метод отсекающих плоскостей, разработанный Р. Гомори, используется при решении полностью целочисленных задач.

В основе комбинаторных методов лежит идея перебора всех допустимых целочисленных решений. Разумеется, на первый план здесь выдвигается проблема разработки процедур, позволяющих непосредственно рассматривать лишь относительно небольшую часть указанных решений, а остальные допустимые решения учитывать некоторым косвенным образом. Наиболее известным комбинаторным методом является метод ветвей и границ.

Дробный алгоритм решения полностью целочисленных задач

Необходимым условием применения данного алгоритма является целочисленность всех коэффициентов и правых частей ограничений исходной задачи. Например, ограничение х1 + (1/3) ×х2 £ 13/2 записывается в виде 6×х1 + 2×х2 £ 39, в котором дроби отсутствуют.

На первом шаге решается задача с ослабленными ограничениями, которая возникает в результате исключения требования целочисленности переменных. Если полученное оптимальное решение оказывается целочисленным, то оно является также решением исходной задачи. В противном случае следует ввести дополнительные ограничения, порождающие (вместе с исходными ограничениями) новую задачу линейного программирования, решение которой оказывается целочисленным и совпадает с оптимальным решением исходной целочисленной задачи.

Пусть последняя симплексная таблица задачи с ослабленными ограничениями имеет следующий вид:

Через xi (i = 1, ..., m) обозначены базисные переменные, а через wj (j = 1, ..., n) – небазисные переменные.

Рассмотрим i-ю строку симплексной таблицы, которой соответствует нецелое значение базисной переменной xi, и выразим xi через небазисные переменные:

, bi – нецелое.

Каждую строку симплексной таблицы, порождающую аналогичное равенство, будем называть производящей строкой.

Пусть bi = + fi, aij = + fij.

Отсюда следует , что

0 < fi < 1, 0 £ fij < 1.

ПРИМЕР

Теперь наше уравнение принимает следующий вид:

Поскольку все переменные xi и wi принимают целые значения, правая часть уравнения должна быть целочисленной, откуда следует, что левая часть уравнения также должна принимать целые значения. Далее, так как fij ³ 0 и wi ³ 0 для всех i и j, то

.

Следовательно, выполняется неравенство .

Это означает, что

, поскольку fi < 1.

Так как левая часть рассматриваемого неравенства должна принимать целые значения, можно записать необходимое условие ее целочисленности в следующем виде:

.

Последнее ограничение перепишем в виде равенства

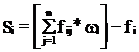, где Si – неотрицательная дополнительная переменная, которая по определению должна принимать целые значения. Такое ограничение-равенство определяет отсечение Гомори для полностью целочисленной задачи.

Из симплексной таблицы следует, что wi = 0, и, таким образом, Si = – fi, т. е. данная компонента решения не является допустимой. Это означает, что полученное ранее решение не удовлетворяет новому ограничению. В такой ситуации следует использовать двойственный симплекс-метод, реализация которого обеспечивает отсечение некоторой области многогранника решений, не содержащей точек с целочисленными координатами.

Преобразуем исходную таблицу путем приписывания к ней строки и столбца, соответствующих построенному отсечению Гомори для полностью целочисленной задачи.

Получим новую таблицу:

Если в результате применения двойственного симплекс-метода решение оказывается целочисленным, то процесс решения исходной задачи завершен. В противном случае необходимо ввести новое отсечение на базе полученной таблицы и вновь воспользоваться двойственным симплекс-методом. Если на некоторой итерации при использовании двойственного симплекс-метода обнаружится отсутствие допустимого решения, то рассматриваемая задача не имеет допустимого целочисленного решения.

Название дробный алгоритм связано с тем обстоятельством, что все ненулевые коэффициенты введенного отсечения меньше единицы. Общее число ограничений порожденной задачи не может превышать (m + n).

Процесс определения оптимального плана методом Гомори включает следующие этапы:

1. Используя симплекс-метод находят решение задачи без учета требований целочисленности переменных.

2. Составляют дополнительное ограничение для переменной, которая в оптимальном плане имеет максимальное дробное значение, а должна быть целочисленной.

3. Используя двойственный симплекс-метод, находят решение задачи, получающейся в результате присоединения дополнительного ограничения.

4. В случае необходимости составляют еще одно дополнительное ограничение и продолжают процесс.

ПРИМЕР

F() = 7×x1 + 9×x2

при ограничениях

-x1 + 3×x2 £ 6  -x1 + 3× x2 + x3 = 6

7×x1 + x2   £ 35  7×x1 + x2 + x4 = 35

x1, х2 ³ 0, целые; x1, ..., x4 ³ 0, целые.

Таблица 1

Так как полученное решение не является целочисленным, следует расширить данную таблицу путем введения некоторого отсечения. В качестве производящей строки можно выбрать любую строку таблицы.         Обычно выбирается строка, соответствующая . Сейчас . Строке с базисной переменной х2 соответствует равенство

x2 + 7/22×x3 + 1/22×x4 = 7/2.

Следовательно, уравнение отсечения Гомори имеет вид

- 7/22×x3 - 1/22×x4 + = -1/2

В результате получаем новую таблицу:

Таблица 2

Так как решение опять не является целочисленным, необходимо продолжить процесс введения отсечений. Строке с базисной переменной х1 соответствует ограничение:

- 1/7×x4 - 6/7× + = -4/7

Таблица 3

В результате получили оптимальное целочисленное решение исходной задачи:

x1 = 4, x2 = 3, F() = 55.

Дадим геометрическую интерпретацию задачи. На рис. 1 показано, что введение двух ограничений позволяет получить новую экстремальную точку с координатами (4;3), в которой достигается оптимум исходной целочисленной задачи.

1 ОТСЕЧЕНИЕ: - 7/22×x3 - 1/22×x4 + S1 = -1/2 или

- 7/22×x3 - 1/22×x4  £ -1/2

Тогда из таблицы 1 получим

-7/22×(х1 - 3×х2 + 6) - 1/22× (-7×x1 - х2 + 35) £ -1/2         Þ

7×(х1 - 3×х2 + 6) + (-7×x1 - х2 + 35) ³ 11       Þ     х2 £  3.

2 ОТСЕЧЕНИЕ:      - 1/7×x4 - 6/7×S1 + S2 = -4/7  или

- 1/7×x4 - 6/7×S1 + S2 £ -4/7

Теперь из таблиц 1 и 2 получим

- 1/7×(-7×x1 - х2 + 35)  - 6/7×(7/22×x3 + 1/22×x4 - 1/2)  £  -4/7    Þ

-1/7×(-7×x1 - х2 + 35) - 6/7× £ -4/7 Þ х1 + х2 £ 7.

Рис. 1. Графическая интерпретация задачи

Современное управление. Энциклопедический справочник. Том второй.:"Издацентр",1997, с разд. 8.

Дж. Риггс Производственные системы: планирование, анализ, контроль., пер. с англ. Общая ред. А.И. Анчишкина.- М.: Прогресс, 1972., с.9.

Мескон М.Х., Альберт М., Хедоури Ф. Основы менеджмента: Пер. с англ.-М.:"Дело", 1992, с. 596..

См., например, Ансофф И. Стратегическое управление.№ пер. с англ.- М.: Экономика,1989; Томпсон А..А., Стрикленд А.Дж. Стратегический менеджмент. Искусство разработки и реализации стратегии: Учебник для вузов/ пер. с англ. Под ред. Л.Г. Зайцева, М.И. Соколовой.- М.: Банки и биржи, ЮНИТИ,1998.

 См., например, Мескон М.Х., Альберт М., Хедоури Ф. Основы менеджмента.- М.:"Дело", 1993.; Герчикова И.Н. Менеджмент.- М.: ЮНИТИ, 1995.

См., например, Лифшиц А.Л., Мальц Э.А. Статистическое моделирование систем массового обслуживания, "Советское радио", 1978.

Смирнов Е.Л. Справочное пособие по НОТ.- М.: Экономика, 1986, с. 177.

См. подробнее Зубов В.М. Как измеряется производительность труда в США.- М.: Финансы и статистика, 1990,

Синк Д.С. Управление производительностью: планирование,измерение и оценка, контроль и повышение; Пер. с англ.- М. Прогресс, 1989.

Англо-русский экономический словарь/ под ред. А.В.Аникина.-М.: Русский язык, 1977,с.365.

В.К.Мюллер Англо-русский словарь.-М.: Русский язык, с.441.

William J. Stevenson Production/Operations Management.-4-th ed., IRWIN, INC., 1993, p.725.

Логистика: Учеб.пособие / под ред. Б.А.Аникина.-М.:ИНФРА-М,1997, с.7.

Там же, с.10.

Там же, с.14.

В экономической литературе выделяют и несколько иные этапы развития логистики: например, дологистический период (до 50-х годов); период классической логистики (60-е годы); период неологистики (с начала 80-х годов). См., например, Логистика /под ред. Б.А.Аникина.-М.: ИНФРА-М,1997,с.31-37.

Производство на заказ может применяться и в условиях дефицита, когда производится сложная и дорогая продукция. В этих условиях целесообразно подождать, пока потребитель точно не изложит свои требования. Например, строить суда или электротурбины на склад не принято. Рельсы же или арматурную сталь производят на склад. То же самое характерно и для продукции, которая имеет множество модификаций (См.: Янош Корнаи Дефицит.-М.: Наука,1990, с.137).

MRP – material requirement planning

Впервые эта система была опробована в 1972 году на автомобильной фирме “Тайота”. Автор системы Т.Оно использовал принцип “последнего звена”, применяемый в супермаркетах, для промышленного производства. В супермаркетах покупатель является информационным источником необходимого количества, ассортимента и т.д. Импульсом для функционирования всей системы служит спрос, определяемый покупателем.

В литературе есть указание, что фонетически более точным является термин “камбан”. См.,например, Статистические методы повышения качества /Под ред. Хитоси Кумэ.- М.: Финансы и статистика, 1990, с. 274.

Янош Корнаи Дефицит.-М.: Наука, 1990, с.139.

Cм. Рис.2.

Подробнее об этом см.: Неруш Ю.М.Коммерческая логистика /учебник.- М.: ЮНИТИ, 1997, с.141.

Подробнее об этом см.: Логистика:Учеб.пособие / Под ред. Б.А.Аникина.-М.:ИНФРА-М,1997,с.237-246.

Неруш Ю.М. Коммерческая логистика/ учебник, М.: ЮНИТИ, 1997, с.143.

Подробнее об этом: Статистическое моделирование и прогнозирование /под ред. А.Г.Гранберга.-М.: Финансы и статистика, 1990, с.184-189.

Промышленная логистика / пер. А.В Проскуряков, Н.К.Моисеева, Н.Т.Севруков, А.Н.Пилищенко.- Санкт-Петербург, Политехника, 1994, с.78-83.

Метод Дельфы получил название от города Дельфы, ставшего известным из-за прорицателей – оракулов, живших в нем и предсказывающих будущее. Пророчества обнародовались после тщательного обсуждения на совете дельфийских мудрецов.

Подробнее о UPC см.: William J. Stevenson Production/Operfnions Management.-4th ed.-RICHARD D. IRWIN, INC., 1993, р.589.

Гаджинский А.М. Основы логистики.-М.:ИВЦ “Маркетинг”, 1996,с.105.

Неруш Ю.М. Коммерческая логистика/ учебник.-М.: ЮНИТИ, 1997, с.165

Логистика /учебное пособие под ред. Б.А.Аникина.-М.: ИНФРА-М. 1997, с. 254.

Гаджинский А.М. Основы логистики (2-е издание).-М.: ИВЦ “Маркетинг”, 1996, с.82.

Там же, с.86.

В настоящее время для внебюджетных предприятий и организаций норматив разрядов рабочих и работ директивно не устанавливается. Предприятие, тем не менее, с учетом имеющегося опыта нормирования, особенностей технологии производства и других факторов, а также в связи с необходимостью оценки затрат труда, его оплаты и т.д. разрабатывает показатели, позволяющие определить и оценить сложность работ самостоятельно. На наш взгляд, применявшаяся ранее 6-ти (в отдельных отраслях 8-ми) разрядная сетка может быть признана наиболее приемлемой, так как не сужает и не размывает диапазон сложности работ по числу разрядов и позволяет соблюдать принцип преемственности экономической информации.

1 На практике перечень дополнительных затрат может быть значительно шире, что увеличивает фактическую себестоимость продукции.

См., например, Фридман П."Контроль затрат и финансовых результатов при анализе качества продукции"– М.: Аудит, ЮНИТИ, 1994 "… возмещенные затраты времени (количество изготовленных единиц изделия, умноженное на нормо-часы)"– с.39. В соответствии с принятой в отечественной экономике терминологией этот показатель носит название"фактического объема производства в нормо-часах».

Значения в рамке приведены с учетом разложения фактора"замена"на составляющие его факторы –"цены"и"нормы».

См."Статистический словарь»– М.: Финанстатинформ, 1996, стр. 268.

  В практике менеджмента распространены три основные формы организационной структуры: функциональная структура; структура по видам продукции; структура, ориентированная на потребителя.