Кривые  и карта безразличия

     Одним из основных инструментов анализа в порядковой теории полезности является кривая безразличия.

            Графически система предпочтений потребителя изображается с помощью кривых безразличия, которые впервые были применены английским экономистом Ф. Эджуортом в 1881 г.

Кривая безразличия – это геометрическое место точек, каждая из которых представляет собой такой набор из двух товаров,  что потребителю безразлично, какой из этих наборов выбрать. Кривая безразличия показывает  альтернативные наборы товаров, обеспечивающие  потребителю одинаковый уровень полезности ( рис. 4).

            На представленной на рис. 4 кривой безразличия выделено четыре точки,  соответствующие четырём равнополезным  для потребителя комбинациям двух благ  (Х и Y).  Эти комбинации товаров дают потребителю одинаковое общее удовлетворение. Комбинации товаров, представляющие для потребителя большую или меньшую полезность, будут находиться выше или ниже представленной на рис. 4       кривой безразличия.

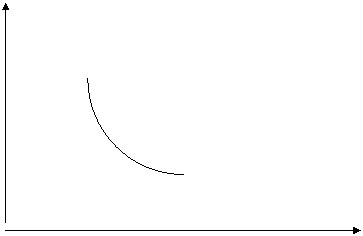Рис. 4.   Кривая безразличия.

Набор кривых безразличия для одного потребителя одной пары товаров образует карту безразличия (рис. 5). Карта безразличия однозначно выражает предпочтения потребителя и позволяет предсказать его отношение к любым двум сочетаниям различных благ.

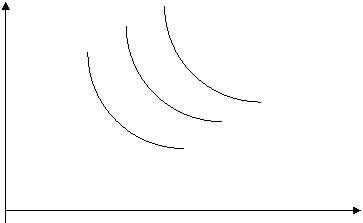Рис. 5.  Карта кривых безразличия.

   Свойства кривых безразличия вытекают из тех гипотез, на которых  базируется порядковая теория полезности.

1.        Кривые безразличия выпуклы к началу координат. Выпуклость кривых безразличия к началу координат означает, что в пределах заданного уровня благосостояния каждая следующая единица уменьшающегося блага равнозначна всё большему количеству увеличивающегося блага.  Это положение иллюстрирует рис.   : чтобы  сохранить данный уровень удовлетворенности (остаться на данной кривой безразличия), каждая следующая порция блага А должна компенсироваться всё  возрастающей порцией блага В.

2.        Кривая безразличия может быть проведена через любую точку пространства товаров, т.е. кривая безразличия не имеет «толщины».

3. Кривая безразличия, более удаленная от начала координат, представляет собой более предпочтительные для потребителя наборы товаров.  Это вытекает из предположения, что большее количество благ предпочтительнее меньшему. Рассмотрим на рис.      кривые безразличия  U1  и   U2. Набор С  содержит такое же количество товара У, что и набор А.  Но набор С  включает большее количество товара Х. Из гипотезы о ненасыщении следует,  что точка С лучше точки А. Все наборы, лежащие на кривой безразличия 1 для потребителя равноценны, так же как и на кривой безразличия 2. Из гипотезы транзитивности следует, что любой набор, лежащий на кривой 2, для потребителя предпочтительнее любого набора, лежащего на кривой 1.

4. Кривые безразличия  не пересекаются.  Предположим, что две кривые безразличия пересекаются в точке А (рис. 6).  Рассмотрим товарные наборы в точках А, В и С.  Наборы А и В  находятся на одной кривой безразличия (         ), следовательно они эквивалентны для потребителя. То же самое можно сказать и о наборах А и С, которые расположены на одной кривой  безразличия (     ).  Из гипотезы транзитивности следует, что  набор  В равноценен набору С. Но набор С  соответствует большему количеству товаров Х и У. Следовательно набор С предпочтительнее набора В. Поскольку потребитель не может одновременно предпочитать  набор С набору В и не делать между ними различия, пересечение двух кривых безразличия означает противоречие. Следовательно, кривые безразличия не могут пересекаться.

Рис. 6. Невозможность пересечения кривых безразличия.

4.    Касательная, проведенная к любой точке кривой безразличия, имеет отрицательный угол наклона.

Рассмотрим точку А (рис. 7) , представляющую определенный набор товаров Х и У. Проведем через неё две взаимно перпендикулярные прямые, которые разделят плоскость координат на четыре квадранта. Все точки, лежащие в Ш квадранте, представляют большие, а все точки, лежащие в 1 квадранте, - меньшее количество товаров Х и У, чем точка А. В соответствии с гипотезой ненасыщения товарные наборы, представленные в Ш квадранте, предпочтительнее набору А, а лежащие в 1 квадранте – менее предпочтительны набору А. Значит, наборы, эквивалентные набору А, должны быть представлены точками, находящимися во П и 1У квадрантах, т.е. кривая безразличия имеет отрицательный наклон.

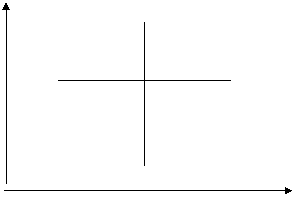
Рис.  7.  Кривые безразличия имеют отрицательный наклон.