Для нерелевантных денежных потоков характерна ситуация, когда отток и приток капитала чередуются. В этом случае некоторые из рассмотренных аналитических показателей с изменением исходных параметров могут меняться в неожиданном направлении, т.е. выводы, сделанные на их основе, могут быть не всегда корректными . Если вспомнить, что IRR является корнем уравнения NPV = 0, а функция NPV = f(r) представляет собой алгебраическое уравнение k-й степени, где k — число лет реализации проекта, то в зависимости от сочетания знаков и абсолютных значений коэффициентов число положительных корней уравнения может колебаться от 0 до k. В частности, если значения денежного потока чередуются по знаку, возможно несколько значений критерия IRR.
Если рассмотреть график функции NPV = f(r, Рk), то возможно различное его представление в зависимости от значений коэффициента дисконтирования и знаков денежных потоков («+» или «–»). Можно выделить две наиболее реальные типовые ситуации (рис. 5.1). Приведенные виды графика функции NPV = f(r, Рk) соответствуют следующим ситуациям:
– имеет место первоначальное вложение капитала с последующими поступлениями денежных средств (рис. 5.1, а);
– имеет место первоначальное вложение капитала, в последующие годы притоки и оттоки капитала чередуются (рис. 5.1, б).
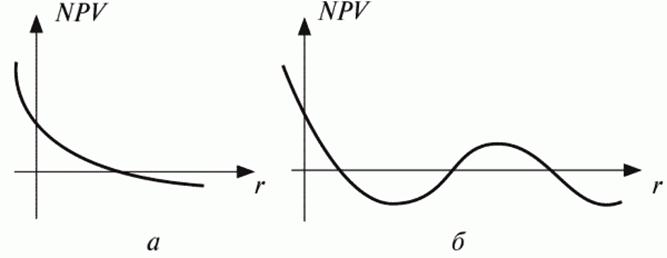
Рис. 5.1. Возможные представления графика NPV = f(r, Pk)
Первая ситуация наиболее типична: она показывает, что функция NPV = f(r) в этом случае является убывающей с ростом r и имеет единственное значение IRR. Во второй ситуации вид графика может быть различным.
Поможем написать любую работу на аналогичную тему

