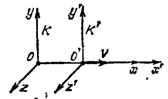
Пусть имеются инерциальные системы отсчета K и K', показанные на рис. На рисунке предполагается, что движется система K', в то время как система K неподвижна. С таким же правом можно считать, что неподвижна система K', а система K движется относительно нее со скоростью —V.
Предположим, что происходит какое-то событие. В системе K. оно характеризуется значениями координат и времени x, у, z, t; в системе K'— значениями координат и времени x', y', z', t'. Найдем формулы связывающие нештрихованные значения со штрихованными. Из однородности пространства и времени следует, что эти формулы должны быть линейными.
При показанном на рис. направлении координатных осей плоскость y' = 0 совпадает с плоскостью y = 0, а плоскость z' = 0 совпадает с плоскостью z = 0. Отсюда вытекает, что, например, координаты y и y' должны обращаться в нуль одновременно, независимо от значений других координат и времени. Это возможно лишь при условии, что
y = α·y',
где вследствие линейности уравнения α ‑ постоянная величина. Ввиду равноправности систем K и K' обратное преобразование должно иметь вид
y'=α· y
с тем же значением а, что и при прямом преобразовании. Перемножив оба соотношения, найдем, что α2 = 1, откуда α = ±1. Для одинаково направленных осей нужно взять α = +1. В результате находим, что
y =y' или y' = y. (1.104)
Аналогичным образом получается формула
z = z' или z' = z. (1.105)
Из этих формул вытекает, что значения y и z не зависят от x' и t', откуда следует, что значения x' и t' не могут зависеть от y и t; соответственно значения x и t не могут зависеть от y' и z'. Это означает, что x и t являются линейными функциями только x' и t'.
Из рис. следует, что точка O имеет координату x = O в системе K и x'= —Vt' в системе K'. Следовательно, выражение x' + Vt' должно обращаться в нуль одновременно с координатой x (когда x' + Vt' равно нулю, x' = —Vt'). Для этого линейное преобразование должно иметь вид
x = γ(x' + Vt'), (1.106)
где γ — константа. Точка O имеет координату x' = 0 в системе K' и x = V·t в системе K. Следовательно, выражение x — V·t должно обращаться в нуль одновременно с координатой x' (когда x — V·t = 0, то x =V·t). Для этого нужно, чтобы выполнялось соотношение
x' = γ(x ‑ Vt). (1.107)
В силу равноправности систем K и K' коэффициент γ в обоих случаях должен быть один и тот же.
Теперь воспользуемся принципом постоянства скорости света. Начнем отсчет времени в обеих системах с того момента, когда начала координат O и O' совпадают. Предположим, что в момент t = t' = 0 в направлении осей x и x' посылается световой сигнал, который производит вспышку света на экране. Это событие (вспышка) характеризуется в системе K координатой x и временем t, а в системе K'— координатой x' и временем t', причем
x = ct, x' =ct'.
(скорость c в обоих случаях одна и та же). Подставив эти значения x и x' в формулы, получим соотношения
ct = γ(ct' + Vt') = γ(c + V)t',
ct' = γ(ct ‑ Vt) = γ (c ‑ V)t.
Перемножив эти соотношения и сократив обе части получившегося равенства на tt', придем к уравнению
c2 = γ2(c2 ‑ V2).
Отсюда
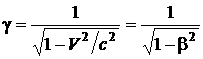, (1.108)
где β = V/c. (1.109)
Подстановка найденного значения у в (1.106) и (1.107) приводит к формулам
, 
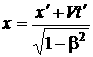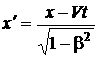. (1.110)
Чтобы найти формулы преобразования времени, исключим из формул (1.110) координату x и разрешим получившееся уравнение относительно t. Затем исключим из формул (1.110) координату x' и разрешим получившееся уравнение относительно t'. В результате придем к формулам
, 
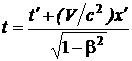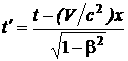(1.111)
Напишем вместе формулы (1.104), (1.105), (1.110) и (1.111), подразделив их на две группы:
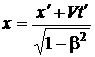, y =y , z = z', 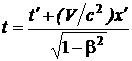, (1.112)
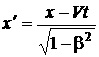, y' = y, z' = z, 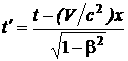. (1.113)
Эти формулы называются преобразованиями Лоренца. По формулам (1.112) осуществляется переход от системы K' к системе K', по формулам (1.113)—переход от системы K к системе K'- Вследствие равноправности систем преобразования (1.112) и (1.113) отличаются лишь знаком перед V Это отличие обусловлено тем, что система K' движется относительно системы K со скоростью V, в то время как система K движется относительно системы K' со скоростью — V.
В преобразованиях Лоренца «перемешаны» координаты и время. Например, время t в системе K определяется не только временем t' в системе K', но также и координатой x'. В этом проявляется взаимосвязь пространства и времени.
В пределе при c ‑» ∞ преобразования Лоренца переходят в преобразования Галилея. Таким образом, различие в течение времени в разных инерциальных системах отсчета обусловлено существованием предельной скорости распространения взаимодействий. При скоростях много меньших скорости света (т. е. при β << 1) преобразования Лоренца практически не отличаются от преобразований Галилея. Следовательно, преобразования Галилея сохраняют значение для скоростей, малых по сравнению со скоростью света.
При V > c выражения для x, t, x' и t' в формулах (1.112) и (1.113) становятся мнимыми. В этом проявляется то обстоятельство, что движение со скоростями, большими с, невозможно. Невозможна даже система отсчета, движущаяся со скоростью с, потому что при V = c знаменатели формул для x и t обращаются в нуль.
Преобразованиям Лоренца можно придать симметричный вид, если написать их для x и ct, т. е. для величин одинаковой размерности. В этом случае формулы преобразований выглядят следующим образом:
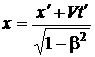, y =y , z = z', 
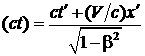, (1.114)
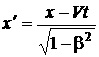, y' = y, z' = z, 
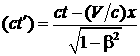. (1.115)
Формулы для x и ct, а также для x' и ct' отличаются друг от друга только перестановкой соответствующих переменных.
Поможем написать любую работу на аналогичную тему