Принцип относительности (равноправие различных инерциальных систем отсчета) ипостулат о постоянстве скорости света во всех инерциальных системах отсчета (независимо от характера движения источника) — два кита на которых покоится стройное здание теории относительности (ТО).
Однако, еще в 1910 годубыло установлено, что постоянство скорости света следует из принципа относительности и общих свойств однородности га лилеева пространства.
В фундаментальной монографии В.А.Фока «Теория пространства, времени и тяготения’’, (М.,1961) на стр. 34—39 показано, что из требования постоянства скорости света вытекает линейность преобразований. В той же работе в Добавлении А (стр. 510—514) доказано, что одно только требование инерциальности систем отсчета приводит к дробно-линейным преобразованиям — в дальнейшем преобразования Лоренца-Фока (LF). Запишем эти преобразования для перехода из системы k в систему k’:
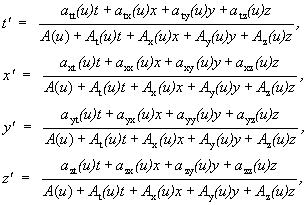 (F1)
(F1)
Здесь u — относительная скорость движения систем отсчета, amn(u), Am(u) и A(u) — функции скорости относительного движения. Знаменатели выражений (F1) могут иметь нули. Требование конечности координат мировых точек во всех инерциальных системах отсчета приводит к упрощению выражения (F1) до обычного линейного преобразования: A(u)=1, все Am(u)=0.
Линейность преобразований Лоренца достигается в галилеевой координатной системе (декартовы координаты и время). Этот факт выделяет галилееву систему координат — делает ее привилегированной.
Требование конечности пространственно-временных координат в различных инерциальных системах отсчета кажется естественным для максимально однородного евклидова пространства. Однако, уже с работы А.Фридмана 1922 года стало ясно, что наше пространство-время может иметь более сложную структуру. Наличие островных масс может приводить к пространственным особенностям, а наличие равномерного распределения масс во всем пространстве приводит к ос обенностям типа Большого Взрыва. Пространство-время, в котором действует группа преобразований Лоренца-Фока (F1), может оказаться полезным в качестве фона на котором разворачиваются сценарии развития реальной вселенной.
В разделе 2 приведен вывод явного вида преобразований Лоренца-Фока, основанный на принципе относительности без постулат а постоянства скорости света.
В разделе 3 рассмотрены различные следстви таких преобразований. Главным из них является относительность бесконечности: бесконечно далекие в пространстве-времени точки оказываютс на конечных расстояниях при переходе в другую инерциальную систему отсчета. В обычных представлениях группы Лоренца временные и пространственные бесконечности остаются таковыми в о всех инерциальных системах отсчета. При преобразованиях Лоренца-Фока бесконечность более не является выделенной инвариантной точкой
Просматривается следующая аналогия с переходом от преобразований Галилея к преобразованиям Лоренца — бесконечно большая скорость — инвариант преобразований Галилея. При преобразованиях Лоренца инвариантна конечная скорость c — некоторая мировая постоянная.
В преобразованиях Лоренца-Фока появляется новая мировая постоянная R размерности длины.
На расстояниях LR и при временах TR/c (как и при стремлении к нулю скорости относительного движения систем отсчета) преобразования Лоренца-Фока переходят в преобразовани Лоренца. Величина R должна, таким образом, соответствовать некоторому космологическому пространственному масштабу.
В этом же разделе показано, что постоянная Хаббла H , т. е. однородная расширяющаяся Вселенная, инвариантна именно относительно преобразований Лоренца-Фока, но не инвариантна относительно преобразования Лоренца.
Поможем написать любую работу на аналогичную тему

