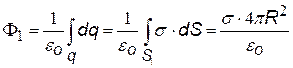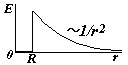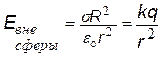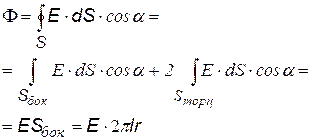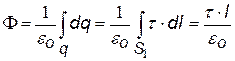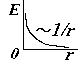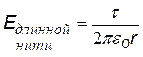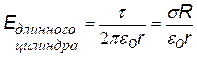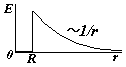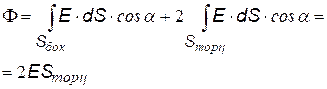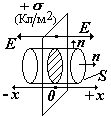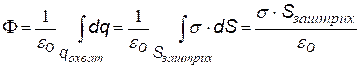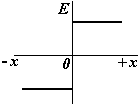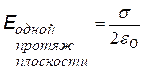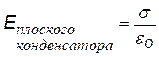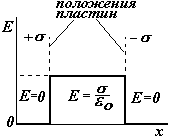Чтобы найти напряженность с помощью теорем Гаусса, нужно взять интеграл. А как его взять, если мы Е еще только пытаемся найти? Кроме того, под интегралом «мешает» cosa. Надо суметь выбрать такую замкнутую поверхность (ее удобно называть гауссовой), в каждой точке которой было бы Е = const, и cosa = const. Тогда в левой части теоремы Е и cosa можно будет вынести из-под знака интеграла. Поэтому практически теорему Гаусса можно применить только в следующих случаях: сфера, шар, длинная нить, длинный цилиндр, бесконечная плоскость.
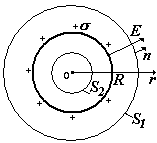
1) Сфера, заряженная с поверхностной плотностью заряда s (Кл/м2)
Рассмотрим области : 1) вне сферы (
) и внутри ее (
). Выберем поверхности: 1) S1 и 2) S2 – обе поверхности – сферы, концентрические с заряженной сферой. Сначала найдем потоки вектора Е
через выбранные поверхности, а затем воспользуемся теоремой.
|
|
Потоки вектора Е
через S1 ( E^n, a = 0, cosa = 1. |
|
|
|
|
по теореме Гаусса; F2 = 0, т.к. S2 не охватывает никаких зарядов. Приравнивая потоки из (¨) и (¨¨), найдем E(r). |
||
|
|
|||
|
q = s×2pR2 – полный заряд сферы |
Вне сферы поле такое же, как поле точечного заряда. На границе сферы происходит скачок напряженности. Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
|
(¨) 
(¨¨)
2)Тонкая длинная нить, заряженная с линейной плотностью заряда t (Кл/м)
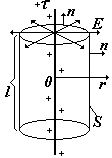
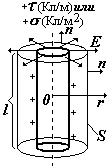
В этом случае «гауссова» поверхность – соосный с нитью цилиндр длиной l.
Сначала найдем поток, потом воспользуемся теоремой Гаусса.
|
|
Разобьем поверхность цилиндра на боковую и две торцевых. Для боковой - cosa = 1, для торцевых - cosa = 0. |
|
|
|
|
по теореме Гаусса; охватываемый заряд – это отрезок нити длиной l. Приравнивая и сокращая, получим E(r). |
||
|
|
|||
|
|
|
3) Тонкостенный длинный цилиндр, заряженный:
1) с линейной плотностью заряда t или
2) с поверхностной плотностью заряда s.
Этот пример аналогичен предыдущему. Выбираем гауссову поверхность в виде соосного цилиндра, разбиваем поверхность на боковую и две торциальные. В первом случае при заданной линейной плотности t получим такую же формулу, как идля длинной нити. Во втором случае охватываемый заряд равен (s×2p×R×l) и формула для E несколько иная, хотя зависимость от r – та же.
|
|
|
|
4) Плоскость, бесконечно протяженная, заряженная с поверхностной плотностью заряда s.
Выберем гауссову поверхность S в виде цилиндра, перпендикулярного заряженной плоскости. Высота цилиндра (2×х/2). Разобьем поверхность на боковую и две торцевых.
|
|
поток через Sбок = 0, т.к.× E^n, a = 90о и cosa = 0 |
|
|
|
|
|
Sзаштрих – площадка с зарядом, охватываемым цилиндром |
|||
|
|
||||
|
|
S заштрих = S торц, т.к. образующие цилиндра перпендикулярны заряженной плоскости. Поле протяженной плоскости – однородное и не зависит от расстояния |
|
||
|
||||
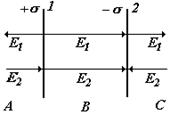
5) Две плоскости, параллельные, разноименно заряженные (плоский конденсатор). В этом случае напряженность поля можно найти по принципу суперпозиции, зная напряженность поля одной плоскости: 
|
|
|
|
|
A) ЕА = Е2 - Е1 = 0 B) ЕВ = Е2 + Е1 =s /eо C) ЕС = Е1 - Е2 =0 |
||
|
Поле плоского конденсатора можно считать однородным с достаточной степенью точности, если расстояние между пластинами значительно больше размеров пластин. |
||
Поможем написать любую работу на аналогичную тему
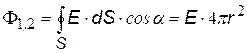