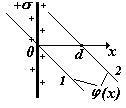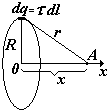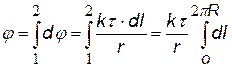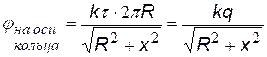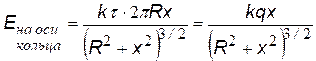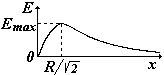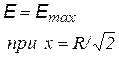Будем рассматривать только случаи, когда напряженность и потенциал зависят только от одной координаты х или радиальной координаты r
для сферически или цилиндрически симметричных тел. Разность потенциалов связана с напряженностью в этом случае как (см. формулу (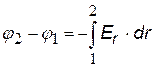 )):
)):
|
|
Связь разности потенциалов с напряженностью для случая одной переменной х или r (математически это уравнение однотипно с ( |
Из уравнений (ª) или (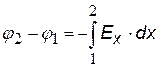 ) можно найти разность потенциалов, если известна функция Е(r) или Е(r). Чтобы получить формулу для потенциала, следует выбрать уровень нулевого потенциала (так же, как в случае потенциальной энергии – см. механику). Обычно принимают j = 0 на бесконечности, но для поля нити это невозможно (см. ниже).
) можно найти разность потенциалов, если известна функция Е(r) или Е(r). Чтобы получить формулу для потенциала, следует выбрать уровень нулевого потенциала (так же, как в случае потенциальной энергии – см. механику). Обычно принимают j = 0 на бесконечности, но для поля нити это невозможно (см. ниже).
1) Точечный заряд.
Подставим в формулу (ª) выражение для напряженности поля точечного заряда. 1 и 2 – любые две точки на радиальной оси координат r. Примем j 1 = 0 при
r1 ®¥, заменим j 2 ® j , r2 ®r получим j (r).
|
|
|
|
|
2).Сфера радиуса R, заряженная с поверхностной плотностью заряда s (Кл/м2).
Полный заряд на сфере q = s×4p×R2 . Будем рассматривать две области:1) ![]() - выбираем две любые точки 1 и 2 в этой области и 2)
- выбираем две любые точки 1 и 2 в этой области и 2) ![]() также выбираем две любые точки уже в этой области. Потенциал должен быть непрерывной функцией, в отличие от напряженности он не может иметь разрывов в данной точке, т.к. по смыслу j - потенциальная энергия единичного положительного заряда, а двух энергий у одного заряда в одной точке данного поля не может быть.
также выбираем две любые точки уже в этой области. Потенциал должен быть непрерывной функцией, в отличие от напряженности он не может иметь разрывов в данной точке, т.к. по смыслу j - потенциальная энергия единичного положительного заряда, а двух энергий у одного заряда в одной точке данного поля не может быть.
|
|
Подставим в (ª) Е поля сферы. Для |
|
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
|
|
|
|
|
|
|
3)Бесконечно длинная нить, заряженная с линейной плотностью заряда t.
Выберем на оси радиальных координат r две любые точки с координатами r1 и r2.
(см. рис.). Подставим в (ª) напряженность поля длинной нити и проинтегрируем.
|
|
В этом случае принять j = 0 на бесконечности нельзя (см. график ln x), поэтому выбираем j = 0 в некоторой произвольной точке с координатой ro. Т.е. примем
заменим j 2 ® j , r2 ®r получим j (r) |
|
|
j = 0 при r = r0 |
|
|
4)Бесконечно протяженная плоскость, равномерно заряженная с поверхностной плотностью заряда s (Кл/м2). Выберем на оси координат х
две произвольные точки х1 и х2 .). Используем формулу связи Е и j (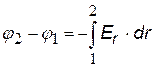 ), подставим выражение для напряженности поля бесконечной плоскости.
), подставим выражение для напряженности поля бесконечной плоскости.
|
|
Чтобы получить выражение для потенциала примем 1)j 1 = 0 при х1 = 0 и 2) j 1 = 0 при х1 = d (d – произвольная точка на оси х) |
|
1) 2) |
|
Следует иметь в виду, что формулы для Е и j в случаях плоскости, нити, цилиндра применимы только на расстояниях от них, существенно меньших размеров этих тел. В действительности при учете краевых эффектов поля становятся более сложными.
Во всех случаях, задавая нулевой уровень потенциала j = 0 в различных точках, мы можем получить сколько угодно формул для потенциала данного поля. Потенциальные кривые (или прямые), т.е. графики j(r)или j(х) при этом будут перемещаться по вертикали параллельно самим себе. В принципе, неважно, где выбрать нулевой уровень потенциала, т.к. во всех задачах имеет значение не сам потенциал, а его изменение
Так как потенциал – скалярная величина, а напряженность – вектор, то значительно проще найти сначала зависимость j(r) или j(х), затем дифференцируя, получить формулу для Е(r)или Е (х).
В качестве примера найдем потенциал поля на оси тонкого кольца, равномерно заряженного с линейной плотностью t, а затем Е (х).Для этого выделим в кольце бесконечно малый элемент dl с зарядом dq = t×dl (см. рис.) В некоторой точке A потенциал складывается из потенциалов, создаваемых всеми элементами кольца.
|
|
потенциал поля элементарного заряда dq (j¥ = 0) |
|
||
|
|
«суммируя» (интегрируя) потенциалы от всех элементов кольца, получим формулу для j (х). |
|||
|
|
Дифференцируя по х, найдем напряженность Е(х) |
|||
|
|
|
|
||
Поможем написать любую работу на аналогичную тему


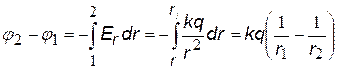
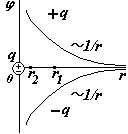
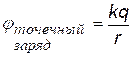 (при j¥ = 0)
(при j¥ = 0)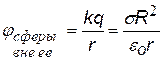 (при j¥ = 0)
(при j¥ = 0) 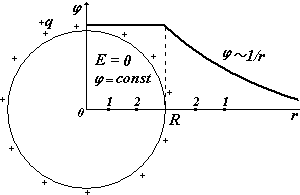
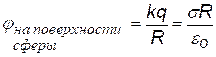
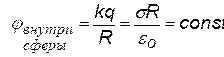
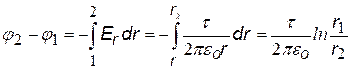
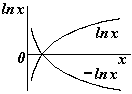 j 1 = 0 при r1 = r0,
j 1 = 0 при r1 = r0,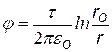
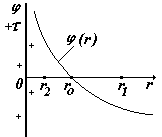
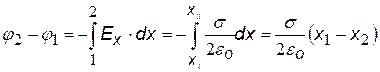
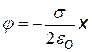 j = 0 при х = 0
j = 0 при х = 0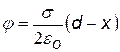 j = 0 при х = d
j = 0 при х = d