Пусть имеется распределение заряда, разобьём заряд на малые элементы объёма dV, в этом элементе объёма заряд 
. 
- это потенциальная энергия заряда в элементе объёма dV, энергия элементарного заряда. Тогда вся потенциальная энергия этого распределения будет равна 
.
Это точная формула. Теперь мы займёмся получением приближённой формулы.
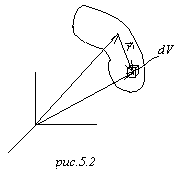
Выберем некоторую точку внутри распределения, радиус-вектор этой точки будет 
, радиус-вектор 
– это вектор, идущий из выбранной точки в этот элемент объёма, 
. Тогда потенциал в точке – это 
. Пока написано разложение с точностью до первых производных, дальше там пойдут слагаемые со вторыми производными и так далее, это факт математический.
В основе этого вычисления лежит следующее предположение: будем считать, что потенциал мало меняется в пределах распределения, то есть распределение не слишком велико. Это означает, что второе слагаемое много меньше первого, то есть значение потенциала в некоторой точке внутри такое-то, а добавка к потенциалу, когда мы доходим до края распределения, мала, поэтому далее слагаемые мы выкидываем вообще. Подставим теперь это дело в формулу для потенциальной энергии: 
.
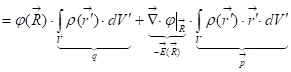Мы добыли вот такую симпатичную формулу: 
, где – радиус-вектор, идущий в некоторую точку внутри распределения, это опять разложение по мультиполям.
Что это физически означает? Главный вклад в потенциальную энергию – полный заряд на значение потенциала где-то внутри распределения, поправочное слагаемое, учитывающее дипольный момент распределения (дипольный момент характеризует как там размещены друг относительно друга отрицательные и положительные заряды), и др. характеристики, учитывающие моменты более высоких порядков.
Чтобы дальше эта буква не вводила в заблуждение, перепишем результат так: 
.
А теперь мы можем найти силу (сила – это градиент потенциальной энергии), пишем: 
. И окончательно получим такой результат:
Поможем написать любую работу на аналогичную тему