1) ![]() Поле заряженной нити
Поле заряженной нити
Рассмотрим равномерно заряженную с линейной плотностью ![]() нить. Представим нить как последовательность элементарных зарядов
нить. Представим нить как последовательность элементарных зарядов ![]() , тогда каждый заряд создает в точке на расстоянии r от него поле, напряженность которого определяется выражением
, тогда каждый заряд создает в точке на расстоянии r от него поле, напряженность которого определяется выражением ![]() .
.
Напряженность можно представить как векторную сумму ее компонент ![]() . Для нахождения поля нити необходимо проинтегрировать данное выражение. Учитывая, что нить симметрична относительно отрезка b, проходящего через ее середину,
. Для нахождения поля нити необходимо проинтегрировать данное выражение. Учитывая, что нить симметрична относительно отрезка b, проходящего через ее середину, ![]() , следовательно,
, следовательно, ![]() .
.
Элементарная напряженность ![]() . Выразим элемент длины нити через расстояние до рассматриваемой точки
. Выразим элемент длины нити через расстояние до рассматриваемой точки ![]() , учитывая, что
, учитывая, что ![]() , перейдем к интегрированию по углам
, перейдем к интегрированию по углам
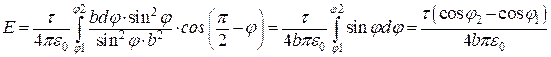
Если нить бесконечная, то j2
= 0, а j1 = p, тогда напряженность поля ![]()
2) Напряженность на оси кольца
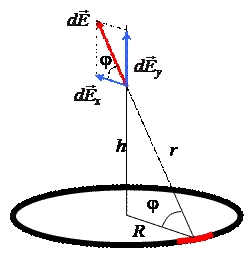 Рассмотрим кольцо радиусом R, равномерно заряженное с линейной плотностью
Рассмотрим кольцо радиусом R, равномерно заряженное с линейной плотностью ![]() . Найдем напряженность поля в точке, расположенной на оси кольца на расстоянии h от его центра.
. Найдем напряженность поля в точке, расположенной на оси кольца на расстоянии h от его центра.
Напряженность поля элементарного заряда ![]() равна
равна ![]() . При интегрировании необходимо учесть осевую симметрию, которая приводит к равенству нулю интеграла
. При интегрировании необходимо учесть осевую симметрию, которая приводит к равенству нулю интеграла ![]() . Из рисунка видно, что
. Из рисунка видно, что ![]() , а
, а ![]() , тогда
, тогда 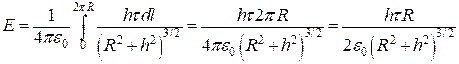 .
.
Чтобы найти напряженность поля в центре кольца положим h = 0, тогда напряженность в центре кольца равна нулю.
3) Бесконечная заряженная плоскость
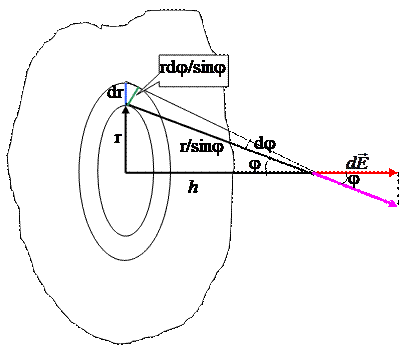 Рассмотрим бесконечную плоскость, заряженную с поверхностной плотностью
Рассмотрим бесконечную плоскость, заряженную с поверхностной плотностью ![]() . Выбираем в качестве элементарного заряда кольцевой слой радиуса r площадью
. Выбираем в качестве элементарного заряда кольцевой слой радиуса r площадью ![]() . Найдем напряженность поля в точке, отстоящей от плоскости на некоторое расстояние h. Так как плоскость бесконечна, то имеет место симметрия относительно перпендикуляра, проведенного к плоскости из точки, в которой будет определена напряженность, поэтому, сохранится только составляющая вектора E, перпендикулярная плоскости.
. Найдем напряженность поля в точке, отстоящей от плоскости на некоторое расстояние h. Так как плоскость бесконечна, то имеет место симметрия относительно перпендикуляра, проведенного к плоскости из точки, в которой будет определена напряженность, поэтому, сохранится только составляющая вектора E, перпендикулярная плоскости.
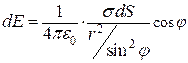 , из рисунка видно, что толщина кольцевого слоя
, из рисунка видно, что толщина кольцевого слоя ![]() .
.
Подставляя значение площади, получим
![]() , проинтегрируем данное выражение в пределах от j1
= p/2 до j2 =0, тогда
, проинтегрируем данное выражение в пределах от j1
= p/2 до j2 =0, тогда 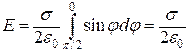
Поможем написать любую работу на аналогичную тему

