Расчет электроемкостей уединенных проводников и конденсаторов

Рассмотрим уединенный шар радиуса R, которому сообщен заряд q. Потенциал на его поверхности равен , тогда электроемкость уединенного шара равна        (2)

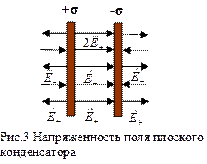
Электроемкость конденсаторов различной формы

1. Рассмотрим плоский конденсатор – две одинаковых проводящих пластины, расположенных близко друг от друга и заряженных с одинаковой поверхностной плотностью σ-=σ+= σ=q/S. Линии напряженности выходят из положительно заряженной пластины и входят в отрицательно заряженную пластину, а модули векторов равны . Сумма напряженностей за пределами пластин равна нулю, а между пластинами Е=2Е+=2Е-. Если расстояние между пластинами d, то напряжение между пластинами равно U=E∙d. Электроемкость плоского конденсатора 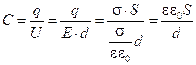 (4)

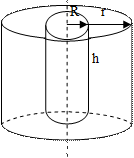2. Рассмотрим цилиндрический конденсатор. Напряженность поля бесконечно длинного цилиндра была найдена по теореме Гаусса и равна . Напряжение между цилиндрами равно 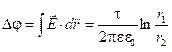. Заряд на каждом из цилиндров равен , тогда емкость цилиндрического конденсатора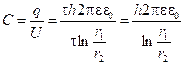

Рассмотрим сферический конденсатор, состоящий из двух разноименно заряженных сфер радиусов r1 и r2. Разность потенциалов между сферами равна , тогда емкость такой системы равна .

Соединение конденсаторов.

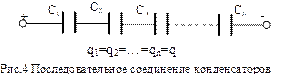Последовательное соединение.

Рассмотрим (рис.4) батарею конденсаторов, соединенных последовательно. Заряды конденсаторов равны друг другу и заряду батареи, а напряжение батареи равно U=U1+U2+…+Un. Запишем формулу (3) для каждого конденсатора и для батареи:

;  =>        

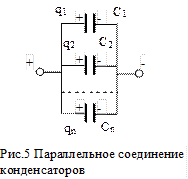Параллельное соединение.

Рассмотрим батарею параллельно соединенных конденсаторов (рис.5). Напряжение на конденсаторах одинаково и равно напряжению батареи U=U1=U2=…=Un, а заряд батареи равен q=q1+q2+…+qn. Для каждого конденсатора запишем формулу (3):

; …

           (6)