Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B,
|
F = IBΔl sin α |
может быть выражена через силы, действующие на отдельные носители заряда.
Пусть концентрация носителей свободного заряда в проводнике есть n, а q – заряд носителя. Тогда произведение nqυS, где υ – модуль скорости упорядоченного движения носителей по проводнику, а S – площадь поперечного сечения проводника, равно току, текущему по проводнику:
|
I = qnυS. |
Выражение для силы Ампера можно записать в виде:
|
F = qnSΔlυB sin α. |
Так как полное число N носителей свободного заряда в проводнике длиной Δl и сечением S равно nSΔl, то сила, действующая на одну заряженную частицу, равна
|
Эту силу называют силой Лоренца. Угол α в этом выражении равен углу между скоростью 
и вектором магнитной индукции 
. Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки.
или по правилу буравчика.
Сила Лоренца направлена перпендикулярно векторам и .
При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется.
Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость 
лежит в плоскости, перпендикулярной вектору , то частица будет двигаться по окружности радиуса
|
Сила Лоренца в этом случае играет роль центростремительной силы.
Период обращения частицы в однородном магнитном поле равен
|
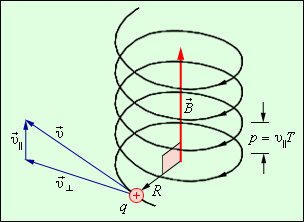
Если скорость частицы 
имеет составляющую 
вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали R зависит от модуля перпендикулярной магнитному полю составляющей υ┴
вектора , а шаг спирали p – от модуля продольной составляющей υ||.
|
|
|
Движение заряженной частицы по спирали в однородном магнитном поле. |
Поможем написать любую работу на аналогичную тему