Интерференция света  методом колец Ньютона

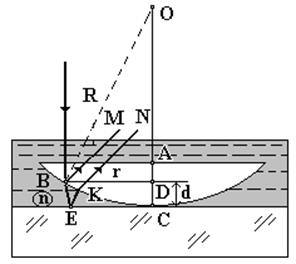
Полосы равной толщины можно наблюдать с помощью установки “Кольца Ньютона” (рис. 2.9, а).

Установка состоит из плоско-выпуклой  стеклянной линзы с радиусом кривизны R, которая выпуклой частью опирается на плоскопараллельную стеклянную пластинку.

Пространство между линзой и пластинкой может быть заполнено жидкостью с абсолютным показателем преломления n (например, для воды n=1,33).

Если на плоскую поверхность линзы падает нормально (перпендикулярно) плоская волна монохроматического света, то в точке В (r=ВD) свет частично преломляется (луч ВЕ) и отражается от  верхней (луч ВМ) и нижней (луч ЕК) поверхностей клина между линзой и пластинкой.

Оптическая разность хода между этими отраженными лучами

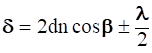                         (2.42)

или       ,                    (2.43)

т.е.        ,                            (2.44)

где cosb=1, т.к. a=b=00.

Здесь учтено, что при отражении света от стекла (nст>nж=n) происходит сдвиг по фазе на p, т.е. появляется дополнительная разность хода .

Из-за невозможности непосредственного измерения величины d, рассмотрим треугольник ОВD, где

       R2 = r2 + OD2,

но       OD = R - d,

т.е.                         r2 =2Rd                    (2.45)

 (d<<R и cлагаемым d2 можно пренебречь).

   Следовательно, .            (2.46)    

С учетом (2.46) оптическую разность хода запишем в виде 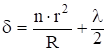         . При dмах = 2m  максимум интерференции на отражение удовлетворяет условию

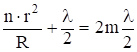
или                                         .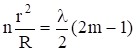

Следовательно, радиус светлого кольца на отражение

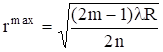                                            .                                           (2.47)

При  dmin = (2m +1) (минимум интерференции на  отражение) радиус темного кольца                           

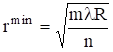                                            .                                                     (2.48)

Аналогичный расчет можно провести для интерференции на просвет. Однако дополнительной оптической разности хода в этом случае не возникает. Поэтому максимум  интерференции в тонких пленках на просвет соответствует условию минимума на отражение - формула (2.48) и, наоборот, минимум интерференции  на просвет соответствует максимуму на отражение - формула (2.47).

Таким образом, при сложении отраженных волн от поверхностей клина возникают интерференционные кольца равной толщины. В центре находится темное пятно (минимум), которое окружено системой чередующихся светлых  (максимум) и темных колец, ширина и интенсивность которых постепенно убывают по мере удаления от центра (рис. 2.9, б).

Так как центральное пятно в отраженном свете - темное, а в проходящем  - светлое, то это доказывает, что при отражении света  от среды с большим показателем преломления фаза отраженной волны меняется на p, а при отражении от среды с меньшим показателем преломления  изменение фазы не происходит.

Это подтверждается специальным опытом Юнга. К пластинке из флинта (n=1,7) прижимают линзу из крона (n=1,5), а пространство между ними заполняют сассафрасовым маслом с промежуточным показателем преломления.  В этом случае фаза волны менялась на p при отражении как от верхней, так и от нижней поверхностей масляной прослойки. Поэтому в центре наблюдается максимум (светлое пятно) в отраженном и минимум (темное пятно)  в проходящем свете.